
【题目】正方形ABCD的CD边长作等边△DCE,AC和BE相交于点F,连接DF.求∠AFD的度数. 
【答案】解:在正方形ABCD和等边三角形DCE中,
∴CB=CD=CE,∠BCD=90°,∠DCE=60°,
∴△BCE是等腰三角形,且∠BCE=90°+60°=150°,
∴∠CBE=15°,
在△BCF和△DCF中,
∵  ,
,
∴△BCF≌△DCF(SAS),
∴∠CBF=∠CDF=15°,
∴∠AFD=∠CDF+∠FCD=15°+45°=60°
【解析】根据等边三角形和正方形的性质证明△BCF≌△DCF,可得结论.
【考点精析】本题主要考查了等边三角形的性质和正方形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图1、图2补充完整;
(3)现有4名学生,其中A类两名,B类两名,从中任选2名学生,求这两名学生为同一类型的概率(用列表法或树状图法).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE. 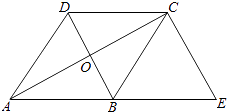
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为确保信息安全,在传输时往往需加密,发送方发出一组密码a,b,c时,则接收方对应收到的密码为A,B,C.双方约定:A=2a﹣b,B=2b,C=b+c,例如发出1,2,3,则收到0,4,5.
(1)当发送方发出一组密码为2,3,5时,则接收方收到的密码是多少?
(2)当接收方收到一组密码2,8,11时,则发送方发出的密码是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】最近几年,某市持续大面积雾霾天气让环保和健康问题成为焦点,为了调查学生对雾霾天气知识的了解程度,某校在全校学生中抽取400名同学做了一次调查,调查结果共分为四个等组A.非常了解;B.比较了解;C.基本了解;D.不了解
根据调查统计结果,绘制了不完整的三种统计图表.
对雾霾天气了解程度的 条形统计图 | 对雾霾天气了解程度的 扇形统计图 | 对雾霾天气了解程度的 统计表 | |
图1 |
图2 | 对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% | ||
B.比较了解 | m | ||
C.基本了解 | 45% | ||
D.不了解 | n | ||
请结合统计图表,回答下列问题:
(1)本次参与调查的学生选择“A.非常了解”的人数为__________人,m=__________,n=__________;
(2)请在图1中补全条形统计图;
(3)请计算在图2所示的扇形统计图中,D部分扇形所对应的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵将折叠的图形恢复原状,点F与BC边上的点G正好重合,连接DG,若AB=6,BC=8,求DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.
(k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.
(1)求反比例函数的表达式
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标
(3)求△PAB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com