Question

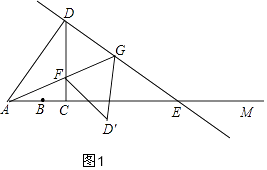
【题目】如图，射线AM上有一点B，AB=6，点C是射线AM上异于B的一点，过C作CD⊥AM，且CD= AC，过D点作DE⊥AD，交射线AM于E，在射线CD取点F，使得CF=CB，连接AF并延长，交DE于点G，设AC=3x．

（1）当C在B点右侧时，求AD．DF的长．（用关于x的代数式表示）
（2）当x为何值时，△AFD是等腰三角形；
（3）作点D关于AG的对称点D′，连接FD′，GD′，若四边形DFD′G是平行四边形，求x的值．（直接写出答案）

Answer 1

【答案】
（1）

解：∵CD= ，AC=3x，

∴CD=4x，

∵CD⊥AM，

∴∠ACD=90°，

由勾股定理得：AD=5x，

∵AB=6，C在B点右侧，

∴BC=AC﹣AB=3x﹣6，

∵BC=FC=3x﹣6，

∴DF=CD﹣FC=4x﹣（3x﹣6）=x+6

（2）

解：分两种情况：

①当C在B点的右侧时，

∴AC＞AB，

∴F必在线段CD上，

∵∠ACD=90°，

∴∠AFD是钝角，若△ADF为等腰三角形，只可能AF=DF，过F作FN⊥AD于N，如图2，

∴AN=ND=2.5x，

cos∠ADC= = ，

，

x= ；

②当C在线段AB上时，同理可知若△ADF为等腰三角形，只可能AF=DF，

i）当CF＜CD时，过F作FN⊥AD于N，如图3，

∵AB=6，AC=3x，

∴BC=CF=6﹣3x，

∴DF=4x﹣（6﹣3x）=7x﹣6，

cos∠ADC= ，

∴ ，

x= ，

ii）当CF＞CD时，如图4，

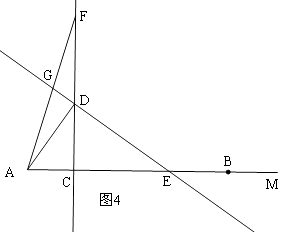
BC=CF=6﹣3x，

∴FD=AD=6﹣3x﹣4x=6﹣7x，

则6﹣7x=5x，

x= ，

综上所述，当x= 或 或 时，△AFD是等腰三角形

（3）

解：∵四边形DFD′G是平行四边形，且DF=D′F，

∴DFD′G是菱形，

∴DF=DG，

∴∠DFG=∠DGF，

∵∠AFC=∠DFG，

∴∠DGF=∠AFC，

∵∠ACD=∠ADG=90°，

∴∠FAC=∠DAG，

即AF平分∠DAC，

过F作FN⊥AD于N，

当C在AB的延长线上时，如图2，

FN=FC=3x﹣6，DF=x+6，

sin∠CDA= ，

解得：x=4，

当C在AB边上时，如图5，

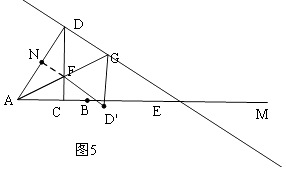
FN=FC=6﹣3x，

DF=7x﹣6，

sin∠CDA= = ，

x= ，

综上所述，若四边形DFD′G是平行四边形，x的值是4或

【解析】（1）由已知条件可得：CD=4x，根据勾股定理得：AD=5x，由AB=6且C在B点右侧，可以依次表示BC、CF、DF的长；（2）分两种情况：①当C在B点的右侧时，AF=DF，②当C在线段AB上时，又分两种情况：i）当CF＜CD时，如图3，ii）当CF＞CD时，如图4，由AF=DF，作等腰三角形的高线FN，由等腰三角形三线合一得：AN=ND=2.5x，利用同角的三角函数列比例式可求得x的值；（3）先根据四边形DFD′G是平行四边形证明它为菱形，由角的关系得：AF平分∠DAC，作辅助线，由角平分线的性质得：FN=FC，根据第2问分两种情况进行计算，根据同角的三角函数列式可求得x的值．