
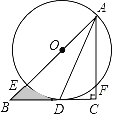
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A,D两点,交AB于点E,交AC于点F
(1)求证:BC是⊙O的切线;
(2)若⊙O半径是2cm,F是弧AD的中点,求阴影部分的面积(结果保留π和根号)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .垂直于
.垂直于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() ,若
,若![]() ,记
,记![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A.5<s<6B.6<s<7C.7<s<8D.8<s<9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)求证:AM是⊙O的切线;
(2)若DC=2,求图中阴影部分的面积.(结果保留π和根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】贺岁片《流浪地球》被称为开启了中国科幻片的大门,2019也被称为中国科幻片的元年.某电影院为了全面了解观众对《流浪地球》的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).根据以上信息,解答下列问题:
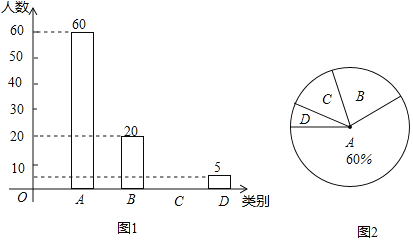
(1)本次接受调查的观众共有 人;
(2)扇形统计图中,扇形C的圆心角度数是 .
(3)请补全条形统计图;
(4)春节期间,该电影院来观看《流浪地球》的观众约3000人,请估计观众中对该电影满意(A、B、C类视为满意)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中.
中.
![]() 利用尺规作图,在BC边上求作一点P,使得点P到AB的距离
利用尺规作图,在BC边上求作一点P,使得点P到AB的距离![]() 的长
的长![]() 等于PC的长;
等于PC的长;
![]() 利用尺规作图,作出
利用尺规作图,作出![]() 中的线段PD.
中的线段PD.
![]() 要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑
要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以![]() 为直径作半圆
为直径作半圆![]() ,点
,点![]() 在半圆上,连结
在半圆上,连结![]() 且
且![]() .连结
.连结![]() 是
是![]() 边上的高,过点
边上的高,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() .
.
![]() 求证:
求证:![]()
![]() 当
当![]() 为
为![]() 的中点时,求
的中点时,求![]() 的值.
的值.
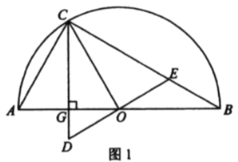
![]() 如图2,取
如图2,取![]() 的中点
的中点![]() ,连结
,连结![]() .若
.若![]() 在点
在点![]() 运动过程中,当四边形
运动过程中,当四边形![]() 的其中一边长是
的其中一边长是![]() 的
的![]() 倍时,求所有满足条件的
倍时,求所有满足条件的![]() 长.
长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F
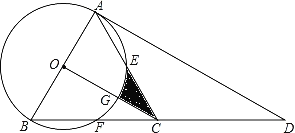
(1)求证:AD是⊙O的切线;
(2)连接OC,交⊙O于点G,若AB=4,求线段CE、CG与![]() 围成的阴影部分的面积S.
围成的阴影部分的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=![]() (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com