
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
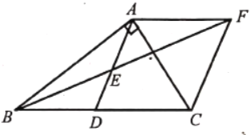
(1)求证:![]() ;
;
(2)证明:四边形![]() 是菱形;
是菱形;
(3)若![]() ,
,![]() ,直接写出菱形
,直接写出菱形![]() 的面积.
的面积.
【答案】(1)见解析;(2)见解析;(3)10
【解析】
(1)根据AAS证![]() AEF≌
AEF≌![]() DEB;
DEB;
(2)利用(1)中全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形,由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出结论;
(3)由直角三角形ABC与菱形有相同的高,根据等积变形求出这个高,代入菱形面积公式可求出结论.
(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,D是BC的中点,
∴AE=DE,BD=CD,
在![]() AFE和
AFE和![]() DBE中,
DBE中,
 ,
,
∴![]() AFE≌
AFE≌![]() DBE(AAS);
DBE(AAS);
(2)证明:由(1)知,![]() AFE≌
AFE≌![]() DBE,
DBE,
则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DC=![]() BC,
BC,
∴四边形ADCF是菱形;
(3)解:连接DF,
∵AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S菱形ADCF=![]() ACDF
ACDF
=![]() ×4×5
×4×5
=10.


科目:初中数学 来源: 题型:
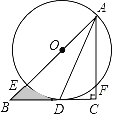
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A,D两点,交AB于点E,交AC于点F
(1)求证:BC是⊙O的切线;
(2)若⊙O半径是2cm,F是弧AD的中点,求阴影部分的面积(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形,![]() 与
与![]() 恰好为对顶角,
恰好为对顶角,![]() ,连接
,连接![]() ,
,![]() ,点F是线段
,点F是线段![]() 上一点.
上一点.
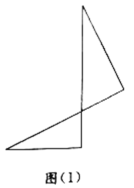
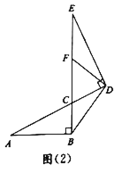
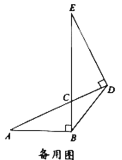
探究发现:
(1)当点F为线段![]() 的中点时,连接
的中点时,连接![]() (如图(2),小明经过探究,得到结论:
(如图(2),小明经过探究,得到结论:![]() .你认为此结论是否成立?_________.(填“是”或“否”)
.你认为此结论是否成立?_________.(填“是”或“否”)
拓展延伸:
(2)将(1)中的条件与结论互换,即:若![]() ,则点F为线段
,则点F为线段![]() 的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
问题解决:
(3)若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文具店有三种品牌的6个笔记本,价格是4,5,7(单位:元)三种,从中随机拿出一个本,已知![]() (一次拿到7元本)
(一次拿到7元本)![]() .
.
(1)求这6个本价格的众数.
(2)若琪琪已拿走一个7元本,嘉嘉准备从剩余5个本中随机拿一个本.
①所剩的5个本价格的中位数与原来6个本价格的中位数是否相同?并简要说明理由;
②嘉嘉先随机拿出一个本后不放回,之后又随机从剩余的本中拿一个本,用列表法求嘉嘉两次都拿到7元本的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为![]() ,若亮亮身高1.70米,则无人机距离地面的高度约为________米.(结果精确到0.1米,参考数据:
,若亮亮身高1.70米,则无人机距离地面的高度约为________米.(结果精确到0.1米,参考数据:![]() ,
,![]() )
)
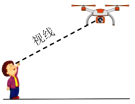
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《郑州市城市生活垃圾分类管理办法》于2019年12月起施行,某社区要投放![]() 两种垃圾桶,负责人小李调查发现:
两种垃圾桶,负责人小李调查发现:
购买数量少于 | 购买数量不少于 | |
| 原价销售 | 以原价的 |
| 原价销售 | 以原价的 |
若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需要付款
个,则共需要付款![]() 元;若购买
元;若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需付款
个,则共需付款![]() 元.
元.
(1)求![]() 两种垃圾桶的单价各为多少元?
两种垃圾桶的单价各为多少元?
(2)若需要购买![]() 两种垃圾桶共
两种垃圾桶共![]() 个,且
个,且![]() 种垃圾桶不多于
种垃圾桶不多于![]() 种垃圾桶数量的
种垃圾桶数量的![]() ,如何购买使花费最少?最少费用为多少元?请说明理由.
,如何购买使花费最少?最少费用为多少元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m,坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E、A、C在同一水平线上,求建筑物BC的高.(结果保留整数,参考数据tan50°=1.1918,cos50°=0.6428)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习《用频率估计概率》这一节课后,数学兴趣小组设计了摸球试验:在一个不透明的盒子里装有质地大小都相同的红球和黑球共![]() 个,将球搅匀后从中随机摸出一个记下颜色,放回,再重复进行下一次试验,下表是他们整理得到的试验数据:
个,将球搅匀后从中随机摸出一个记下颜色,放回,再重复进行下一次试验,下表是他们整理得到的试验数据:
摸球的次数 |
|
|
|
|
|
|
摸到红球的次数 |
|
|
|
|
|
|
摸到红球的频率 |
|
|
|
|
|
|
(1)试估计:盒子中有红球 个;
(2)若从盒子中一次性摸出两个球,用画树状图或列表的方法求出一次性摸出的两个球都是红球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com