
【题目】在学习《用频率估计概率》这一节课后,数学兴趣小组设计了摸球试验:在一个不透明的盒子里装有质地大小都相同的红球和黑球共![]() 个,将球搅匀后从中随机摸出一个记下颜色,放回,再重复进行下一次试验,下表是他们整理得到的试验数据:
个,将球搅匀后从中随机摸出一个记下颜色,放回,再重复进行下一次试验,下表是他们整理得到的试验数据:
摸球的次数 |
|
|
|
|
|
|
摸到红球的次数 |
|
|
|
|
|
|
摸到红球的频率 |
|
|
|
|
|
|
(1)试估计:盒子中有红球 个;
(2)若从盒子中一次性摸出两个球,用画树状图或列表的方法求出一次性摸出的两个球都是红球的概率.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、
、![]() .
.
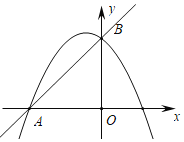
(1)求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的值.
的值.
(2)当![]() 时,若
时,若![]() 的函数值随
的函数值随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
(3)如图,当![]() 时,在抛物线上是否存在点
时,在抛物线上是否存在点![]() ,使
,使![]() 的面积为1?若存在,请求出符合条件的所有点
的面积为1?若存在,请求出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).

(1)求反比例函数的关系式;
(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
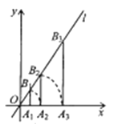
【题目】如图,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,
为圆心,![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ;再过点
;再过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,
为圆心,![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ,...,按此做法进行下去,则
,...,按此做法进行下去,则![]() 的长是______.
的长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 是线段
是线段![]() 上的一个动点.设点
上的一个动点.设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
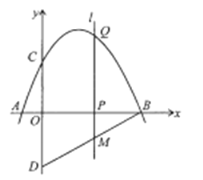
(1)求抛物线的解析式;
(2)连接![]() ,
,![]() ,当点
,当点![]() 运动到何处时,
运动到何处时,![]() 面积最大?最大面积是多少?并求出此时点
面积最大?最大面积是多少?并求出此时点![]() 的坐标;
的坐标;
(3)在第![]() 问的前提下,在
问的前提下,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 值最小,求出
值最小,求出![]() 的最小值并直接写出此时点
的最小值并直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是射线
是射线![]() 上一点,
上一点,![]() .动点
.动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 水平向左作匀速运动,与此同时,动点
水平向左作匀速运动,与此同时,动点![]() 从点
从点![]() 出发,也以
出发,也以![]() 的速度沿
的速度沿![]() 竖直向上作匀速运动.连接
竖直向上作匀速运动.连接![]() ,交
,交![]() 于点
于点![]() .经过
.经过![]() 、
、![]() 、
、![]() 三点作圆,交
三点作圆,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .设运动时间为
.设运动时间为![]() ,其中
,其中![]() .
.
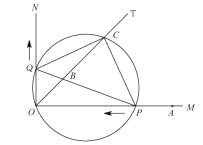
(1)求![]() 的值;
的值;
(2)是否存在实数![]() ,使得线段
,使得线段![]() 的长度最大?若存在,求出
的长度最大?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
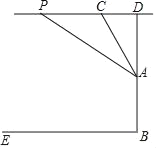
【题目】如图,滑翔运动员在空中测量某寺院标志性高塔“云端塔”的高度,空中的点P距水平地面BE的距离为200米,从点P观测塔顶A的俯角为33°,以相同高度继续向前飞行120米到达点C,在C处观测点A的俯角是60°,求这座塔AB的高度(结果精确到1米).(参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
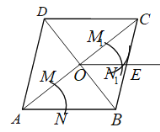
【题目】如图,菱形![]() 的对角线
的对角线![]() 相交于点
相交于点![]() 按下列步骤作图:①以点
按下列步骤作图:①以点![]() 为圆心,任意长为半径作弧,分别交
为圆心,任意长为半径作弧,分别交![]() 于点
于点![]() ;②以点
;②以点![]() 为圆心,
为圆心,![]() 长为半径作弧,交
长为半径作弧,交![]() 于点
于点![]() ;③点
;③点![]() 为圆心,
为圆心,![]() 以长为半径作弧,在
以长为半径作弧,在![]() 内部交②中所作的圆弧于点
内部交②中所作的圆弧于点![]() ;④过点
;④过点![]() 作射线
作射线![]() 交
交![]() 于点
于点![]() .
.![]() ,四边形
,四边形![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com