
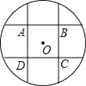
【题目】如图,边长为2的正方形ABCD各边的延长线和反向延长线与⊙O的交点把⊙O分成8条相等的弧,则⊙O的半径是_____.
【答案】![]()
【解析】
连接MN,EW,MW,QM,证四边形QMNW和BWNC是矩形,推出WN=QM=EW=2,根据勾股定理求出BE=BW=![]() ,在Rt△MQW中根据勾股定理求出半径即可.
,在Rt△MQW中根据勾股定理求出半径即可.
解:连接MN,EW,MW,QM,
∵弧QM=弧WN,
∴QM∥WN,QM=WN,∠WNM=![]() ×360°×4×
×360°×4×![]() =90°,
=90°,
∴四边形QMNW是矩形,
∴O在MW上,
∵正方形ABCD,
∴∠WBC=∠BCN=90°,
∴四边形BCNW是矩形,
∴WN=QM=EW=2,
∵∠BEW=∠EWB=45°,
∴由勾股定理得:EB=BW=![]() ,
,
同理AQ=![]() ,
,
设圆O的半径是r,
在Rt△MQW中,由勾股定理得:MQ2+QW2=MW2,
∴22+(![]() )2=(2r)2
)2=(2r)2
r=![]() ,
,
故答案为: ![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
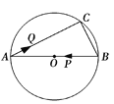
【题目】如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60°.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q以1cm/s的速度从A点出发沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有2部不同的电影A、B,甲、乙、丙3人分别从中任意选择1部观看.
(1)求甲选择A部电影的概率;
(2)求甲、乙、丙3人选择同一部电影的概率(请用画树状图的方法给出分析过程,并求出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
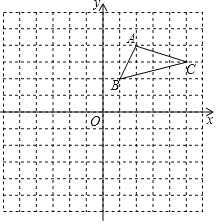
【题目】在如图所示的方格纸(每个小方格都是边长为1个单位的正方形)中建立平面直角坐标系,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点B1的坐标;
(2)画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2;
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ∥
∥![]() ,⊙O与
,⊙O与![]() 和
和![]() 分别相切于点A和点B.点M和点N分别是
分别相切于点A和点B.点M和点N分别是![]() 和
和![]() 上的动点,MN沿
上的动点,MN沿![]() 和
和![]() 平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
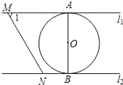
A. ![]() B. l1和l2的距离为2
B. l1和l2的距离为2
C. 若∠MON=90°,则MN与⊙O相切 D. 若MN与⊙O相切,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
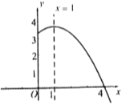
【题目】抛物线![]() 的部分图像如图所示,抛物线的对称轴是直线
的部分图像如图所示,抛物线的对称轴是直线![]() ,与
,与![]() 轴的一个交点坐标为(4,0).下列结论中:①
轴的一个交点坐标为(4,0).下列结论中:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④抛物线与
有两个不相等的实数根;④抛物线与![]() 轴的另一个交点坐标为(–1,0);⑤若点
轴的另一个交点坐标为(–1,0);⑤若点![]() 在该抛物线上,则
在该抛物线上,则![]() .其中正确的有( )
.其中正确的有( )
A. ①③④ B. ②③④ C. ①③⑤ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数![]() 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;
(2)当![]() 时,y<0;
时,y<0;
(3)二次函数![]() 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.
则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
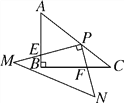
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4.Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
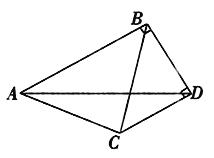
【题目】如图,△ABD和△BDC都是直角三角形,且∠ABD=∠BDC=90°,∠BAD=30°,∠DBC=45°,则tan∠DAC的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com