
【题目】二次函数![]() (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数![]() 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;
(2)当![]() 时,y<0;
时,y<0;
(3)二次函数![]() 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.
则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,BD是△ABC的角平分线,P是射线AC上任意一点 (不与A. D. C三点重合),过点P作PQ⊥AB,垂足为Q,交直线BD于E.

(1)如图①,当点P在线段AC上时,说明∠PDE=∠PED.
(2)作∠CPQ的角平分线交直线AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,而
的小数部分我们不可能全部写出来,而![]() <2于是可用
<2于是可用![]() 来表示
来表示![]() 的小数部分.请解答下列问题:
的小数部分.请解答下列问题:
(1)![]() 的整数部分是_______,小数部分是_________;
的整数部分是_______,小数部分是_________;
(2)如果![]() 的小数部分为
的小数部分为![]() 的整数部分为
的整数部分为![]() 求
求![]() 的值;
的值;
(3)已知:![]() 其中
其中![]() 是整数,且
是整数,且![]() 求
求![]() 的平方根。
的平方根。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连接PQ交边AC于点D,则DE的长为( )

A.![]() B.
B.![]() C.
C.![]() D.不能确定
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:已知如图,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,且
,且![]() .
.

求证:![]() .
.
证明:![]() 平分
平分![]() (__________)
(__________)
![]() (__________)
(__________)
![]() 平分
平分![]() (已知)
(已知)
![]() ____________(角的平分线的定义).
____________(角的平分线的定义).
![]() ___________
___________ ![]() ___________
___________![]() (____________)
(____________)
![]() (___________),
(___________),
![]() ____________(___________)
____________(___________)
![]() (___________).
(___________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电超市经营甲、乙两种品牌的洗衣机.经投标发现,1台甲品牌冼衣机进价比1台乙品牌洗衣机进价贵500元;购进2台甲品牌洗衣机和3台乙品牌洗衣机共需进货款13500元.
(1)购进1台甲品牌洗衣机和1台乙品牌洗衣机进价各需要多少元?
(2)超市根据经营实际情况,需购进甲、乙两种品牌的洗衣机总数为50台,购进甲、乙两种品牌的洗衣机的总费用不超过145250元.
①请问甲品牌洗衣机最多购进多少台?
②超市从经营实际需要出发,其中甲品牌洗衣机购进的台数不少于乙晶牌冼衣机台数的3倍,则该超市共有几种购进方案?试写出所有的购进方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
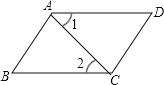
【题目】 根据题意,完成推理填空:如图,AB∥CD,∠1=∠2,试说明∠B=∠D.
解:∵∠1=∠2(已知)
∴ (內错角相等,两直线平行)
∴∠BAD+∠B=180°(两直线平行,同旁内角互补)
∵AB∥CD
∴ + =180°,
∴∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
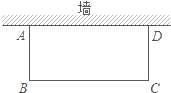
【题目】校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
(1)能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.
(2)若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到x,y轴的距离中的最大值等于点Q到x,y轴的距离中的最大值,则称P,Q两点为“等距点”图中的P,Q两点即为“等距点”.

(1)已知点A的坐标为![]() .①在点
.①在点![]()
![]()
![]() 中,为点A的“等距点”的是________;②若点B的坐标为
中,为点A的“等距点”的是________;②若点B的坐标为![]() ,且A,B两点为“等距点”,则点B的坐标为________.
,且A,B两点为“等距点”,则点B的坐标为________.
(2)若![]()
![]() 两点为“等距点”,求k的值.
两点为“等距点”,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com