
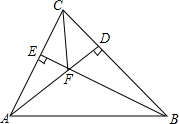
 如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,AD、BE相交于点F,连接CF.
如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,AD、BE相交于点F,连接CF.分析 三角形的高即从三角形的一个顶点向它的对边引垂线,顶点和垂足间的线段.根据概念可求解各小题.
解答 解:(1)在△ABC中,AC边上的高为BE,BC边上的高为AD;
(2)在△ABD中,AD边上的高为BD;
(3)在△BCE中,CE边上的高为BE;
(4)在△BCF中,BC边上的高为FD;
(5)在△ABF中,AF边上的高为BD,BF边上的高为AE.
故答案为BE,AD;BD;BE;FD;BD,AE.
点评 本题考查了三角形的高,由定义可知,三角形的高是线段,线段的两个端点一个是三角形的顶点,另一个是垂足.注意:锐角三角形的三条高在三角形内部,相交于三角形内一点;直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | p=0,q=0 | B. | p=0,q≠0 | C. | p≠0,q=0 | D. | p≠0,q≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com