
分析 根据多边形的内角和公式(n-2)•180°可知多边形的内角和是180°的倍数,然后用1000°÷180°所得商的整数部分加1就是多边形的边数,即可求多边形的内角和,即可解答.
解答 解:设多边形的边数是n,则(n-2)•180°=1000°,
解得n=7…100°,
∵除去了一个内角,
∴边数是7+1=8,
这个多边形的边数为8,
多边形的内角和为;(8-2)×180°=1080°,
则∠A=1080°-1000°=80°,
故答案为:80°.
点评 本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.同时要注意每一个内角都应当大于0°而小于180度.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
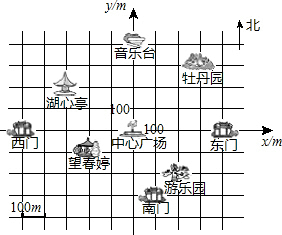 星期天,小明、小刚、小红三名同学到公园玩时走散了,以中心广场为坐标原点,以正东、正北方向为x轴、y轴正方向建立坐标系,他们对着景区示意图通过电话互报出了自己的位置(图中小正方形的边长代表100m).
星期天,小明、小刚、小红三名同学到公园玩时走散了,以中心广场为坐标原点,以正东、正北方向为x轴、y轴正方向建立坐标系,他们对着景区示意图通过电话互报出了自己的位置(图中小正方形的边长代表100m).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com