
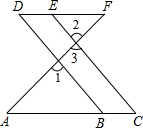
 如图所示,已知在四边形BCED中,A是CB延长线上的点,连接AF,如果∠1=∠2,∠C=∠D,请说明AC∥DF.
如图所示,已知在四边形BCED中,A是CB延长线上的点,连接AF,如果∠1=∠2,∠C=∠D,请说明AC∥DF.  通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题
 如图,A,B两港间距离为74km,一轮船从离A港10km的P地出发向B港匀速行驶,30min后离A港26km(未到达B港),设出发xh后,轮船离A港ykm(未到达B港).
如图,A,B两港间距离为74km,一轮船从离A港10km的P地出发向B港匀速行驶,30min后离A港26km(未到达B港),设出发xh后,轮船离A港ykm(未到达B港).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2+$\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2-$\frac{\sqrt{2}}{2}$ | D. | -$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
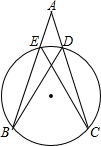 如图,∠A=40°,且$\widehat{BE}$=$\widehat{BC}$=$\widehat{CD}$,则∠ACE的度数为15°.
如图,∠A=40°,且$\widehat{BE}$=$\widehat{BC}$=$\widehat{CD}$,则∠ACE的度数为15°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
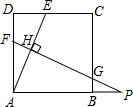 如图,在正方形ABCD中,边长AD=12,点E是边CD上的动点(点E不与端点C、D重合),AE的垂直平分线FP分别交AD、AE、BC于点F、H、G,交AB的延长线于点P.
如图,在正方形ABCD中,边长AD=12,点E是边CD上的动点(点E不与端点C、D重合),AE的垂直平分线FP分别交AD、AE、BC于点F、H、G,交AB的延长线于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com