
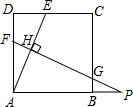
 如图,在正方形ABCD中,边长AD=12,点E是边CD上的动点(点E不与端点C、D重合),AE的垂直平分线FP分别交AD、AE、BC于点F、H、G,交AB的延长线于点P.
如图,在正方形ABCD中,边长AD=12,点E是边CD上的动点(点E不与端点C、D重合),AE的垂直平分线FP分别交AD、AE、BC于点F、H、G,交AB的延长线于点P.分析 (1)延长AE、BC交于点K,则KE=AE,AH=$\frac{1}{3}$HK,然后证明△AHF∽△KHC,根据相似三角形的对应边的比相等求解;
(2)过点G作GQ⊥AD于点Q,过点H作HM⊥AD于点M,证明△FHM∽△FGQ,根据相似三角形的对应边的比相等求解;
(3)首先求得m的值,根据S四边形DEHF=S△ADE-S△AHF即可求解.
解答 解:(1)延长AE、BC交于点K.
∵AD∥BC,
∴△ADE∽△KCE,
又∵DE=EC,
∴KE=AE,
又∵HE=AH,
∴AH=$\frac{1}{3}$HK,即$\frac{AH}{HK}$=$\frac{1}{3}$.
∵AD∥BC,
∴△AHF∽△KHC,
∴$\frac{FH}{HG}$=$\frac{AH}{HK}$=$\frac{1}{3}$.
故答案是:$\frac{1}{3}$;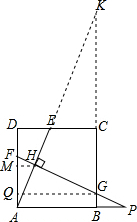
(2)过点G作GQ⊥AD于点Q,过点H作HM⊥AD于点M.
∵FP垂直平分AE,
∴AH=EH.
∵MH∥CD∥AB,
∴AM=MD,
∴MH=$\frac{1}{2}$DE=$\frac{1}{2}$m.
∵QG=AB=AD=12,MH∥GQ,
∴△FHM∽△FGQ,
∴$\frac{FH}{FG}$=$\frac{MH}{QG}$=$\frac{\frac{1}{2}m}{12}$=$\frac{m}{24}$.
∴$\frac{FH}{HG}$=$\frac{m}{24-m}$.
(3)当$\frac{FH}{FG}$=$\frac{1}{2}$,$\frac{m}{24-m}$=$\frac{1}{2}$,
解得:m=8.
∵FG=AE=$\sqrt{{8}^{2}+1{2}^{2}}$=4$\sqrt{13}$,
∴FH=$\frac{m}{24}$•FG=$\frac{1}{3}$×$\sqrt{{8}^{2}+1{2}^{2}}$=$\frac{4\sqrt{13}}{3}$.
∵AH=$\frac{1}{2}$AE$\sqrt{13}$.
∴S△ADE=$\frac{1}{2}$AD•DE=48,S△AHF=$\frac{1}{2}$AH•FH=$\frac{1}{2}$×2$\sqrt{13}$×$\frac{4\sqrt{13}}{3}$=$\frac{52}{3}$,
∴S四边形DEHF=48-$\frac{52}{3}$=$\frac{92}{3}$.
点评 本题是相似三角形的判定与性质以及勾股定理、正方形的性质的综合应用,正确作出辅助线,作出相似的三角形是关键.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
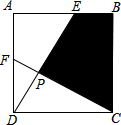 如图,在面积为3的正方形ABCD中,E,F分别是AB和AD上的点,DE⊥CF于点P,且DF=1,S△DPF=$\frac{\sqrt{3}}{8}$,
如图,在面积为3的正方形ABCD中,E,F分别是AB和AD上的点,DE⊥CF于点P,且DF=1,S△DPF=$\frac{\sqrt{3}}{8}$,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
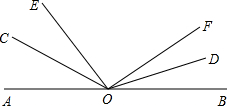 喜羊羊、美羊羊在微信建立了一个学习讨论组,现在他们讨论了一道关于角的和与差的题,如图.
喜羊羊、美羊羊在微信建立了一个学习讨论组,现在他们讨论了一道关于角的和与差的题,如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com