
【题目】在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,点
,点![]() 的对应点分别是
的对应点分别是![]() ,连接
,连接![]() 线段
线段![]() 与线段
与线段![]() 交于点M,连接
交于点M,连接![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图1,求证:OM平分![]() ;
;
(3)如图2,若![]() ,求
,求![]() 的长.
的长.

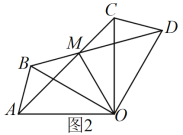
【答案】(1)见详解;(2)见详解;(3)![]()
【解析】
(1)根据旋转的性质及OA=OB可得OA=OC=OB=OD,∠AOC=∠BOD,然后根据“SAS”证明△AOC≌△BOD即可得证;
(2)过点O作OE⊥AC,OF⊥BD,利用等积法可得OE=OF,再根据“HL”可证得Rt△MOE≌Rt△MOF即可得证;
(3)过点M作MH⊥AO,由![]() 可得∠OAC=∠ODB=45°,进而可证得△AOM≌△DOM,则∠MOD=∠MOA,利用
可得∠OAC=∠ODB=45°,进而可证得△AOM≌△DOM,则∠MOD=∠MOA,利用![]() 及
及![]() 可得∠MOA=60°,设OH=x,利用30°、45°的直角三角形的性质及勾股定理可表示出MO、MH、AH、AM的长,根据
可得∠MOA=60°,设OH=x,利用30°、45°的直角三角形的性质及勾股定理可表示出MO、MH、AH、AM的长,根据![]() 列出方程求解,进而可求得CM的长.
列出方程求解,进而可求得CM的长.
(1)证明:∵旋转,
∴OA=OC,OB=OD,∠AOC=∠BOD,
∵OA=OB,
∴OA=OC=OB=OD,
在△AOC与△BOD中,
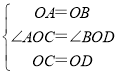
∴△AOC≌△BOD(SAS),
∴AC=BD;
(2)证明:过点O作OE⊥AC,OF⊥BD,垂足分别为E、F,
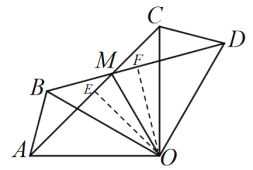
∵△AOC≌△BOD,
∴S△AOC=S△BOD,
∵OE⊥AC,OF⊥BD,
∴![]() ,
,
∵AC=BD,
∴OE=OF,
∵OE⊥AC,OF⊥BD,
∴∠MEO=∠MFO=90°,
在Rt△MOE与Rt△MOF中,
![]()
∴Rt△MOE≌Rt△MOF(HL),
∴∠OME=∠OMF,
∴OM平分![]() ;
;
(3)解:过点M作MH⊥AO,垂足为点H,
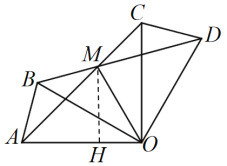
∵![]() ,OA=OC,OB=OD,
,OA=OC,OB=OD,
∴∠OAC=∠ODB=45°,
在△AOM与△DOM中,
∴△AOM与△DOM(AAS),
∴∠AOM =∠DOM,
∵∠BOD=![]() ,∠AOB=30°,
,∠AOB=30°,
∴∠AOM =∠DOM=60°,
∵MH⊥AO,
∴∠MHO=∠MHA=90°,
∴在Rt△MHO中,∠OMH=30°,
设OH=x,则MO=2OH=2x,
∴![]() ,
,
∴在Rt△MHA中,∠HAM=45°,
∴AH=MH=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
解得:x=2,
∴![]() ,
,
在Rt△AOC中,![]() ,
,
∴![]() ,
,
∴CM的长为![]() .
.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】在一个装有2个红球和3个白球(每个球除颜色外完全相同)的盒子中任意摸出一个球,摸到红球小明获胜,摸到白球小刚获胜,这个游戏对双方公平吗?为什么?如何修改可以让游戏公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与x轴有交点.
与x轴有交点.
(1)求m的取值范围;
(2)如果该二次函数的图像与x轴的交点分别为(x1,0),(x2,0),且2 x1 x2+ x1+ x2≥20,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.
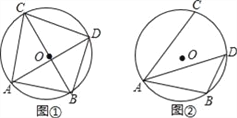
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b的图象与反比例函数y=![]() 的图象的两个交点;
的图象的两个交点;
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com