
【题目】如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6 ![]() ,∠BAD=60°,且AB>6
,∠BAD=60°,且AB>6 ![]() .
.
(1)求∠EPF的大小;
(2)若AP=10,求AE+AF的值;
(3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值.
【答案】
(1)
解:过点P作PG⊥EF于点G,如图1所示.
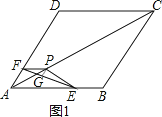
∵PE=PF=6,EF=6 ![]() ,
,
∴FG=EG=3 ![]() ,∠FPG=∠EPG=
,∠FPG=∠EPG= ![]() ∠EPF.
∠EPF.
在Rt△FPG中,sin∠FPG= ![]() =
= ![]() =
= ![]() ,
,
∴∠FPG=60°,
∴∠EPF=120°.
(2)
解:过点P作PM⊥AB于点M,作PN⊥AD于点N,如图2所示.
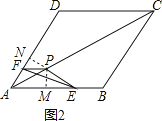
∵AC为菱形ABCD的对角线,
∴∠DAC=∠BAC,AM=AN,PM=PN.
在Rt△PME和Rt△PNF中,PM=PN,PE=PF,
∴Rt△PME≌Rt△PNF,
∴ME=NF.
又AP=10,∠PAM= ![]() ∠DAB=30°,
∠DAB=30°,
∴AM=AN=APcos30°=10× ![]() =5
=5 ![]() ,
,
∴AE+AF=(AM+ME)+(AN﹣NF)=AM+AN=10 ![]()
(3)
解:如图,
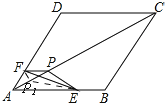
当△EFP的三个顶点分别在AB,AD,AC上运动,点P在P1,P之间运动,
∴P1O=PO=3,AO=9,
∴AP的最大值为12,AP的最小值为6
【解析】(1)根据锐角三角函数求出∠FPG,最后求出∠EPF.(2)先判断出Rt△PME≌Rt△PNF,再根据锐角三角函数求解即可,(3)根据运动情况及菱形的性质判断求出AP最大和最小值.此题是菱形的性质题,主要考查了菱形的性质,锐角三角函数,特殊角的三角函数,解本题的关键是作出辅助线.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知整数a1 , a2 , a3 , a4 , …满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2012的值为( )
A.﹣1005
B.﹣1006
C.﹣1007
D.﹣2012
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( ) 
A.75°36′
B.75°12′
C.74°36′
D.74°12′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=2 ![]() ,求PD的长.
,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=﹣ ![]() x与反比例函数y=
x与反比例函数y= ![]() 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3. 
(1)求反比例函数的表达式;
(2)将直线y=﹣ ![]() x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com