
【题目】如图,直线y=kx+b与x轴、y轴分别交于点A,B,且OA=8,OB=6,P点是第一象限内直线y=kx+b上的一个动点(点P不与点A,B重合),点P的横坐标为m.

(1)求直线AB的解析式.
(2)C是x轴上一点,且OC=2,求△ACP的面积S与m之间的函数关系式;
(3)在x轴上是否有在点Q,使以A,B,Q为顶点的三角形是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x+6;(2)S=﹣
x+6;(2)S=﹣![]() m+12或S=﹣3m+24(0<m<8);(3)存在,点Q的坐标为:(18,0)或(﹣2,0)或(﹣8,0)或(
m+12或S=﹣3m+24(0<m<8);(3)存在,点Q的坐标为:(18,0)或(﹣2,0)或(﹣8,0)或(![]() ,0)
,0)
【解析】
(1)由已知可得A(8,0)、B(0,6),把点A、B的坐标代入一次函数表达式:y=kx+b,即可求直线AB的表达式为:y=﹣![]() x+6;
x+6;
(2)设点P(m,﹣![]() m+6),当点C在x正半轴时,OC=2,AC=4,S=
m+6),当点C在x正半轴时,OC=2,AC=4,S=![]() ×4×(﹣
×4×(﹣![]() m+6)=﹣
m+6)=﹣![]() m+12;当点C在x轴负半轴时,可得:S=﹣3m+24;
m+12;当点C在x轴负半轴时,可得:S=﹣3m+24;
(3)设点Q(s,0),则AB2=100,AQ2=(8﹣s)2,BQ2=s2+36,①当AB=AQ时,100=(8﹣s)2,解得:s=18或s=﹣2;②当AB=BQ时,100=s2+36,可得:s=±8(舍去8);③当AQ=BQ时,(8﹣s)2=s2+36,可得:s=![]() .
.
解:(1)∵OA=8,OB=6,
∴A(8,0)、B(0,6),
把点A、B的坐标代入一次函数表达式:y=kx+b,
∴b=6,k=﹣![]() ,
,
∴直线AB的表达式为:y=﹣![]() x+6;
x+6;
(2)设点P(m,﹣![]() m+6),
m+6),
当点C在x正半轴时,OC=2,AC=4,S=![]() ×4×(﹣
×4×(﹣![]() m+6)=﹣
m+6)=﹣![]() m+12;
m+12;
当点C在x轴负半轴时,同理可得:S=﹣3m+24,
故S=﹣![]() m+12或S=﹣3m+24(0<m<8);
m+12或S=﹣3m+24(0<m<8);
(3)设点Q(s,0),
则AB2=100,AQ2=(8﹣s)2,BQ2=s2+36,
①当AB=AQ时,100=(8﹣s)2,解得:s=18或s=﹣2;
②当AB=BQ时,100=s2+36,可得:s=±8(舍去8);
③当AQ=BQ时,(8﹣s)2=s2+36,可得:s=![]() ,
,
综上,点Q的坐标为:(18,0)或(﹣2,0)或(﹣8,0)或(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)当x为何值时,y>0?当x为何值时,y<0?
(3)写出y随x的增大而减小的自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京世界园艺博览会(简称“世园会”)园区2019年4月29日至2019年10月7日在中国北京市延庆区举行,门票价格如表:小明全家于9月28日集体入园参观游览,通过计算发现:若提前两天线上购买门票所需费用为996元,而入园当天购票所需费用为1080元,则该家庭中可以购买优惠票的有_____人.
票种 | 票价(元/人) | |
指定日 | 普通票 | 160 |
优惠票 | 100 | |
平日 | 普通票 | 120 |
优惠票 | 80 | |
注1:“指定日”为开园日(4月29日)、五一劳动节(5月1日)、端午节、中秋节、十一假期(含闭园日),“平日”为世园会会期除“指定日”外的其他日期;
注2:六十周岁及以上老人、十八周岁以下的学生均可购买优惠票;
注3:提前两天及以上线上购买世园会门票,票价可打九折,但仅限于普通票.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-4x+3.
(1)用配方法求其图象的顶点C的坐标,并描述该函数的函数值随自变量的增减而变化的情况;
(2)求函数图象与x轴的交点A,B的坐标,及△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,A(2,4),B(4,1),C(-3,4)

(1)平移线段AB到线段CD,使点A与点C重合,写出点D的坐标.
(2)直接写出线段AB平移至线段CD处所扫过的面积.
(3)平移线段AB,使其两端点都在坐标轴上,则点A的坐标为
查看答案和解析>>
科目:初中数学 来源: 题型:
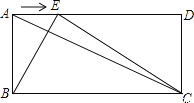
【题目】(14分)如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
(1)若a=5,AC=13,求b.
(2)若a=5,b=10,当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.

(1)求证:AD平分∠BAC;
(2)求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com