
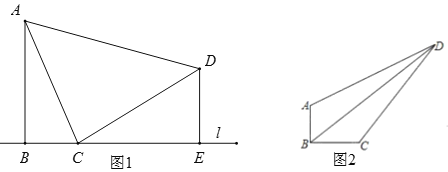
【题目】(1)如图1,已知AB⊥l,DE⊥l,垂足分别为B、E,且C是l上一点,∠ACD=90°.求证:△ABC∽△CED;
(2)如图2,在四边形ABCD中,∠ABC=90°,AB=6,BC=8,CD=20,DA=![]() .求BD的长为_______.
.求BD的长为_______.
【答案】(1)证明见解析;(2)4![]() .
.
【解析】
(1)先证明∠BAC=∠DCE,根据相似三角形的判定△ABC∽△CED即可;
(2)利用勾股定理和相似三角形的判定和性质解答即可.
(1)∵AB⊥l,DE⊥l,∴∠ABC=∠CED=90°,∠ACB+∠BAC=90°.
∵∠ACD=90°,∴∠ACB+∠DCE=90°,∴∠BAC=∠DCE,∴△ABC∽△CED;
(2)如图,连接AC.过点D作DE⊥BC延长线于点E.
∵∠ABC=90°,∴AC![]() .
.
∵AD=10![]() ,CD=20,∴△ACD满足AC2+CD2=AD2,∴∠ACD=90°.
,CD=20,∴△ACD满足AC2+CD2=AD2,∴∠ACD=90°.
由(1)得:△ABC∽△CED,∴![]() ,∴CE=12,DE=16.
,∴CE=12,DE=16.
在Rt△BDE中,BD![]() .
.

故答案为:![]() .
.


科目:初中数学 来源: 题型:
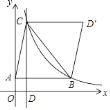
【题目】如图,在△ABC中,B、C两点恰好在反比例函数y= ![]() (k>0)第一象限的图象上,且BC=
(k>0)第一象限的图象上,且BC= ![]() ,S△ABC=
,S△ABC= ![]() ,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为________.
,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于 x 的一元二次方程 x![]() ﹣(m+2)x+3m﹣3=0.
﹣(m+2)x+3m﹣3=0.
(1)求证:方程总有两个实数根;
(2)若方程有一个根小于-2,求 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
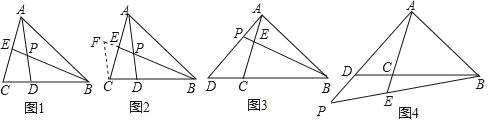
【题目】阅读下面材料:小昊遇到这样一个问题:如图1,在△ABC中,BE是AC边上的中线,点D在BC边上,![]() ,AD与BE相交于点P,求
,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点C作CF∥AD,交BE的延长线于点F,通过构造△CEF,经过推理和计算能够使问题得到解决(如图2).
请回答:写出![]() 的值.
的值.
参考小昊思考问题的方法,解决问题:
(1)如图3,在△ABC中,点D在BC的延长线上,![]() ,点E在AC上,且
,点E在AC上,且![]() .求
.求![]() 的值;
的值;
(2)如图4,在△ABC中,点D在BC的延长线上,![]() ,点E在AC上,且
,点E在AC上,且![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
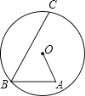
【题目】如图,在O内有折线OABC,点B、C在圆上,点A在O内,其中OA=4cm,BC=14cm,∠A=∠B=![]() ,则AB的长为__________________
,则AB的长为__________________
查看答案和解析>>
科目:初中数学 来源: 题型:
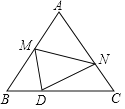
【题目】如图,等边△ABC的边长为30,点M为线段AB上一动点,将等边△ABC沿过点M的直线折叠,使点A落在直线BC上的点D处,且BD∶DC=1∶4,折痕与直线AC交于点N,则AN的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx﹣c经过直线y=x﹣3与坐标轴的两个交点A,B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)点P为抛物线上的一个动点,求使S△APC:S△ACD=5:4的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道![]() 上确定点D,使CD与
上确定点D,使CD与![]() 垂直,测得CD的长等于21米,在
垂直,测得CD的长等于21米,在![]() 上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
(1)求AB的长(精确到0.1米,参考数据:![]() );
);
(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.
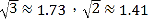
查看答案和解析>>
科目:初中数学 来源: 题型:
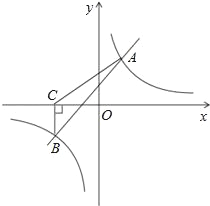
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(2,3),B(﹣3,n)两点.
的图象相交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com