练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

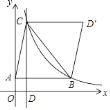
    【题目】如图，在△ABC中，B、C两点恰好在反比例函数y= （k＞0）第一象限的图象上，且BC= ，S△ABC= ，AB∥x轴，CD⊥x轴交x轴于点D，作D关于直线BC的对称点D′．若四边形ABD′C为平行四边形，则k为________．

    【答案】88

    【解析】

    设AB交CD于H．首先证明B、C关于直线y=x对称，设C（a，b），则B（b，a），想办法列出方程求出k即可.

    解：设AB交CD于H．

    由题意AB=CD′=CD，
    ∴B、C两点关于直线y=x对称，设C（a，b），则B（b，a），
    ∵S△ABC= ，
    ∴ b（b-a）=，

    ∵ab=k，
    ∴b=2 ，a= ,

    ∴CH=BH= ，
    ∵BC= ，
    ∴BC=BH，
    ∴= ，

    解得k=8．
    故答案为8．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，在矩形ABCD中，P为CD边上一点（DP<CP），∠APB=90°.将ΔADP沿AP翻折得到，PD′的延长线交边AB于点M，过点B作BN‖MP交DC于点N.

    图1

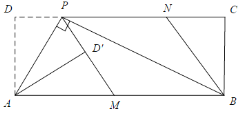
    图2

    （1）求证：；

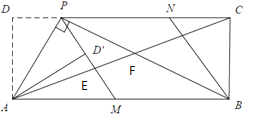
    （2）请判断四边形PMBN的形状，并说明理由；

    （3）如图2，连接AC，分别交PM，PB于点E，F.若tan∠PAD=，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，□ABCD，BE//DF，且分别交对角线AC于点E，F，连接ED，BF .

    求证：(1)ΔABE≌ΔCDF；

    (2)∠DEF=∠BFE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

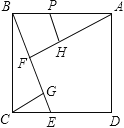
    【题目】如图，在正方形ABCD中，过B作一直线与CD相交于点E，过A作AF垂直BE于点F，过C作CG垂直BE于点G，在FA上截取FH=FB，再过H作HP垂直AF交AB于P．若CG=3．则△CGE与四边形BFHP的面积之和为　_________　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

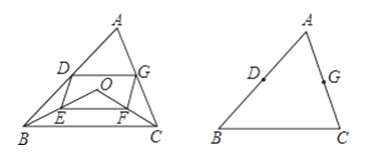
    【题目】点O是三角形ABC所在平面内一动点，连接OB、OC，并将AB、OB、OC、AC中点D、E、F、G，依次连接起来，设DEFG能构成四边形．

    （1）如图，当点O在△ABC内时，求证：四边形DEFG是平行四边形；

    （2）当点O在△ABC外时，（1）的结论是否成立？（画出图形，指出结论，不需说明理由；）

    （3）若四边形DEFG是菱形，则点O的位置应满足什么条件？试说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

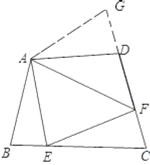
    【题目】如图，若在四边形ABCD中，AB=AD，∠B+∠D=180°．E、F分别是BC、CD上的点，且∠EAF=∠BAD，延长FD到点G，使DG=BE，连接AG，下列结论：①△ABE≌△ADG；②△AEF≌△AGF；③EF=BE+DF；④AD+BE＞AF，正确的有__________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

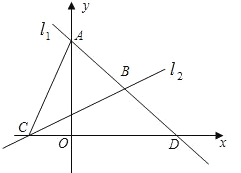
    【题目】如图，直线l1过点A（0，4），点D（4，0），直线l2：与x轴交于点C，两直线，相交于点B．

    （1）求直线的解析式和点B的坐标；

    （2）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠BAC=90°，AD⊥BC，∠ABC的平分线BE交AD于点F，AG平分∠DAC.给出下列结论：①∠BAD=∠C； ②∠AEF=∠AFE； ③∠EBC=∠C；④AG⊥EF．正确结论有（ ）

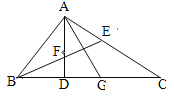
    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

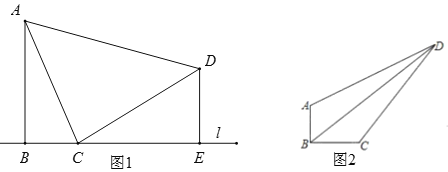
    【题目】（1）如图1，已知AB⊥l，DE⊥l，垂足分别为B、E，且C是l上一点，∠ACD=90°．求证：△ABC∽△CED；

    （2）如图2，在四边形ABCD中，∠ABC=90°，AB=6，BC=8，CD=20，DA=．求BD的长为_______．

    查看答案和解析>>

    同步练习册答案