
【题目】如图,已知抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0)两点,且交y轴交于点C.
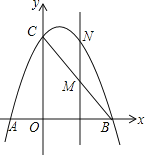
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B、C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点M,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.
【答案】(1)y=﹣x2+2x+3;(2)MN=﹣m2+3m(0<m<3);(3)存在,当m=![]() 时,△BNC的面积最大,最大值为
时,△BNC的面积最大,最大值为![]()
【解析】
(1)直接利用待定系数法即可求出抛物线的解析式;
(2)先利用待定系数法求出直线BC的解析式,已知点M的横坐标,代入直线BC、抛物线的解析式中,可得到M、N点的坐标,N、M纵坐标的差的绝对值即为MN的长;
(3)根据题(1)(2)的结论,列出![]() 关于m的表达式,再利用函数的性质求解
关于m的表达式,再利用函数的性质求解![]() 的最大值即可.
的最大值即可.
(1)抛物线![]() 经过点
经过点![]() 两点,代入得:
两点,代入得:
![]() ,解得:
,解得:![]()
则抛物线的解析式为![]() ;
;
(2)由抛物线![]() 可知,
可知,![]()
因此,设直线BC的解析式为:![]()
代入![]() 得
得![]()
解得:![]()
则直线BC的解析式:![]()
已知点M的横坐标为m,且![]() 轴,则
轴,则![]() ;
;
则![]()
故MN的长为![]() ;
;
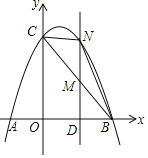
(3)存在点M,使![]() 的面积最大
的面积最大
如图,过点M作![]() 轴于点D
轴于点D
则![]()
即![]()
![]()
由二次函数的性质可知:当![]() 时,
时,![]() 随m的增大而增大;当
随m的增大而增大;当![]() 时,
时,![]() 随m的增大而减小
随m的增大而减小
则当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】成都市某景区经营一种新上市的纪念品,进价为20元/件,试营销阶段发现;当销售单价是30元时,每天的销售量为200件;销售单价每上涨2元,每天的销售量就减少10件.这种纪念品的销售单价为x(元).
(1)试确定日销售量y(台)与销售单价为x(元)之间的函数关系式;
(2)若要求每天的销售量不少于15件,且每件纪念品的利润至少为30元,则当销售单价定为多少时,该纪念品每天的销售利润最大,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.据统计,当每辆车的月租金为3000元时,可全部租出.每辆车的月租金每增加50元时,未租出的车将会增加1辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的租金定为多少元时,租赁公司的月收益(租金收入扣除维护费)可达到306600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
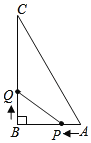
【题目】如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/秒的速度移动,同时点Q从B点开始沿BC边向点C以2cm/秒的速度移动,且当其中一点到达终点时,另一个点随之停止移动.
(1)P,Q两点出发几秒后,可使△PBQ的面积为8cm2.
(2)设P,Q两点同时出发移动的时间为t秒,△PBQ的面积为Scm2,请写出S与t的函数关系式,并求出△PBQ面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
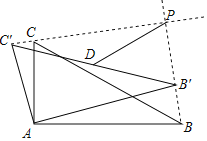
【题目】如图,将水平放置的三角板ABC绕直角顶点A逆时针旋转,得到△AB'C',连结并延长BB'、C'C相交于点P,其中∠ABC=30°,BC=4.
(1)若记B'C'中点为点D,连结PD,则PD=_____;
(2)若记点P到直线AC'的距离为d,则d的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形OABC的边长为5,且tan∠AOC=![]() ,点E是线段BC的中点,过点A、E的抛物线y=ax2+bx+c与边AB交于点D.
,点E是线段BC的中点,过点A、E的抛物线y=ax2+bx+c与边AB交于点D.
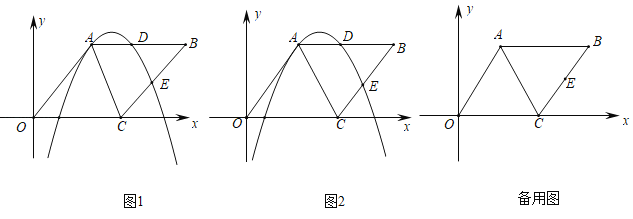
(1)求点A和点E的坐标;
(2)连结DE,将△BDE沿着DE翻折.
①当点B的对应点B'恰好落在线段AC上时,求点D的坐标;
②连接OB、BB',请直接写出此时该抛物线二次项系数a= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径做圆,与BC相切于点C,过点A作AD⊥BO交BO的廷长线于点D,且∠AOD=∠BAD.

(1)求证:AB为⊙O的切线;
(2)若BC=6,tan∠ABC=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
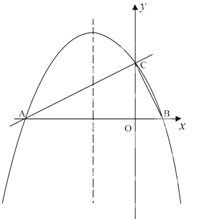
【题目】如图,在平面直角坐标系xoy中,直线![]() 与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是
与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是![]() 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com