
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœBΘΫ90ΓψΘ§ABΘΫ6cmΘ§BCΘΫ8cmΘ§ΒψP¥”AΒψΩΣ Φ―ΊAB±ΏœρΒψB“‘1cm/ΟκΒΡΥΌΕ»“ΤΕ·Θ§Ά§ ±ΒψQ¥”BΒψΩΣ Φ―ΊBC±ΏœρΒψC“‘2cm/ΟκΒΡΥΌΕ»“ΤΕ·Θ§«“Β±Τδ÷–“ΜΒψΒΫ¥ο÷’Βψ ±Θ§Νμ“ΜΗωΒψΥφ÷°ΆΘ÷Ι“ΤΕ·Θ°
Θ®1Θ©PΘ§QΝΫΒψ≥ωΖΔΦΗΟκΚσΘ§Ω… ΙΓςPBQΒΡΟφΜΐΈΣ8cm2Θ°
Θ®2Θ©…ηPΘ§QΝΫΒψΆ§ ±≥ωΖΔ“ΤΕ·ΒΡ ±ΦδΈΣtΟκΘ§ΓςPBQΒΡΟφΜΐΈΣScm2Θ§«κ–¥≥ωS”κtΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ωΓςPBQΟφΜΐΒΡΉν¥σ÷ΒΘ°
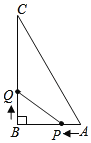
ΓΨ¥πΑΗΓΩΘ®1Θ©Ψ≠Ιΐ2Μρ4ΟκΚσΘ§ΓςPBQΒΡΟφΜΐΒ»”Ύ8cm2Θ°Θ®2Θ©‘Ύ“ΤΕ·Ιΐ≥Χ÷–Θ§ΓςPBQΒΡΉν¥σΟφΜΐ «9cm2Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©”…Χβ“βΘ§Ω……ηPΓΔQΨ≠ΙΐtΟκΘ§ ΙΓςPBQΒΡΟφΜΐΈΣ8cm2Θ§‘ρPB=6-tΘ§BQ=2tΘ§ΗυΨί»ΐΫ«–ΈΟφΜΐΒΡΦΤΥψΙΪ ΫΘ§SΓςPBQ=![]() BPΓΝBQΘ§Ν–≥ω±μ¥ο ΫΘ§Ϋβ¥π≥ωΦ¥Ω…ΘΜ
BPΓΝBQΘ§Ν–≥ω±μ¥ο ΫΘ§Ϋβ¥π≥ωΦ¥Ω…ΘΜ
Θ®2Θ©”…Χβ“βΘ§Ω……ηPΓΔQΨ≠ΙΐtΟκΘ§‘ρPB=6-tΘ§BQ=2tΘ§ΗυΨί»ΐΫ«–ΈΟφΜΐΒΡΦΤΥψΙΪ ΫΘ§SΓςPBQ=![]() BPΓΝBQΘ§Ν–≥ω±μ¥ο ΫΘ§»ΜΚσ«σ≥ωΚ· ΐΒΡΉν¥σ÷ΒΦ¥Ω….
BPΓΝBQΘ§Ν–≥ω±μ¥ο ΫΘ§»ΜΚσ«σ≥ωΚ· ΐΒΡΉν¥σ÷ΒΦ¥Ω….
ΫβΘΚΘ®1Θ©…ηΨ≠ΙΐtΟκΚσΘ§ΓςPBQΒΡΟφΜΐΒ»”Ύ8cm2Θ°
![]() ΓΝΘ®6©¹tΘ©ΓΝ2tΘΫ8Θ§
ΓΝΘ®6©¹tΘ©ΓΝ2tΘΫ8Θ§
ΫβΒΟΘΚt1ΘΫ2Θ§t2ΘΫ4Θ§
¥πΘΚΨ≠Ιΐ2Μρ4ΟκΚσΘ§ΓςPBQΒΡΟφΜΐΒ»”Ύ8cm2Θ°
Θ®2Θ©“άΧβ“βΘ§ΒΟSΘΫ![]() ΓΝPBΓΝBQΘΫ
ΓΝPBΓΝBQΘΫ![]() ΓΝΘ®6©¹tΘ©ΓΝ2tΘΫ©¹t2+6tΘΫ©¹Θ®t©¹3Θ©2+9Θ§
ΓΝΘ®6©¹tΘ©ΓΝ2tΘΫ©¹t2+6tΘΫ©¹Θ®t©¹3Θ©2+9Θ§
Γύ‘Ύ“ΤΕ·Ιΐ≥Χ÷–Θ§ΓςPBQΒΡΉν¥σΟφΜΐ «9cm2Θ°


 ÷ά≠ ÷»Ϊ”≈ΝΖΩΦΨμœΒΝ–¥πΑΗ
÷ά≠ ÷»Ϊ”≈ΝΖΩΦΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥…Χ≥ΓΦΤΜ°Ψ≠œζAΓΔBΝΫ÷÷–¬–ΆΫΎΡήΧ®ΒΤΙ≤50’ΒΘ§’βΝΫ÷÷Χ®ΒΤΒΡΫχΦέΓΔ έΦέ»γœ¬±μΥυ ΨΘ°
A–Ά | B–Ά | |
ΫχΦέΘ®‘Σ/’ΒΘ© | 40 | 65 |
έΦέΘ®‘Σ/’ΒΘ© | 60 | 100 |
Θ®1Θ©»τΗΟ…Χ≥ΓΙΚΫχ’β≈ζΧ®ΒΤΙ≤”Ο»Ξ2500‘ΣΘ§Έ ’βΝΫ÷÷Χ®ΒΤΗςΙΚΫχΕύ…Ό’ΒΘΩ
Θ®2Θ©‘ΎΟΩ÷÷Χ®ΒΤœζ έάϊ»σ≤Μ±δΒΡ«ιΩωœ¬Θ§»τΗΟ…Χ≥Γœζ έ’β≈ζΧ®ΒΤΒΡΉήάϊ»σ≤Μ…Ό”Ύ1400‘ΣΘ§Έ ÷Ν…Ό–ηΙΚΫχB÷÷Χ®ΒΤΕύ…Ό’ΒΘΩ
Θ®3Θ©»τΗΟ…Χ≥Γ‘ΛΦΤ”Ο≤Μ…Ό”Ύ2500‘Σ«“≤ΜΕύ”Ύ2600‘ΣΒΡΉ ΫπΙΚΫχ’β≈ζΧ®ΒΤΘ§ΈΣΝΥ¥ρΩΣB÷÷Χ®ΒΤΒΡœζ¬ΖΘ§…Χ≥ΓΨωΕ®ΟΩ έ≥ω“Μ’ΒB÷÷Χ®ΒΤΘ§ΖΒΜΙΙΥΩΆœ÷Ϋπa‘ΣΘ®10ΘΦaΘΦ20Θ©Θ§Έ ΗΟ…Χ≥ΓΗΟ»γΚΈΫχΜθΘ§≤≈ΡήΜώΒΟΉν¥σΒΡάϊ»σΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΫχ“Μ≤ΫΧαΗΏ»ΪΟώΓΑΫΎ‘Φ”ΟΥ°Γ±“β ΕΘ§Ρ≥―ß–ΘΉι÷·―ß…ζΫχ––Φ“ΆΞ‘¬”ΟΥ°ΝΩ«ιΩωΒς≤ιΜνΕ·Θ§άνΟςΥφΜζ≥ι≤ιΝΥΥυΉΓ–Γ«χxΜßΦ“ΆΞΒΡ‘¬”ΟΥ°ΝΩΘ§Μφ÷ΤΝΥœ¬Οφ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘΚ

Θ®1Θ©«σx≤Δ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®2Θ©«σ’βxΜßΦ“ΆΞΒΡ‘¬ΤΫΨυ”ΟΥ°ΝΩΘΜ≤ΔΙάΦΤάνΟςΥυΉΓ–Γ«χ620ΜßΦ“ΆΞ÷–‘¬”ΟΥ°ΝΩΒΆ”Ύ‘¬ΤΫΨυ”ΟΥ°ΝΩΒΡΦ“ΆΞΜß ΐΘΜ
Θ®3Θ©¥”‘¬”ΟΥ°ΝΩΈΣ5m3ΚΆ9m3ΒΡΦ“ΆΞ÷–»Έ―ΓΝΫΜßΫχ––”ΟΥ°«ιΩωΈ ΨμΒς≤ιΘ§«σ―Γ≥ωΒΡΝΫΜß÷–‘¬”ΟΥ°ΝΩΈΣ5m3ΚΆ9m3«ΓΚΟΗς”–“ΜΜßΦ“ΆΞΒΡΗ≈¬ ΘΜ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏy=ax2+bx+3Ψ≠ΙΐA(3Θ§0)Θ§B(1Θ§0)ΝΫΒψ(»γΆΦ1)Θ§ΕΞΒψΈΣM.
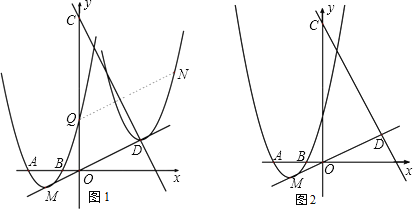
(1)aΓΔbΒΡ÷ΒΘΜ
(2)…η≈ΉΈοœΏ”κy÷αΒΡΫΜΒψΈΣQ(»γΆΦ1)Θ§÷±œΏy=2x+9”κ÷±œΏOMΫΜ”ΎΒψD. œ÷ΫΪ≈ΉΈοœΏΤΫ“ΤΘ§±Θ≥÷ΕΞΒψ‘Ύ÷±œΏOD…œ.Β±≈ΉΈοœΏΒΡΕΞΒψΤΫ“ΤΒΫDΒψ ±Θ§QΒψ“Τ÷ΝNΒψΘ§«σ≈ΉΈοœΏ…œΒΡΝΫΒψMΓΔQΦδΥυΦ–ΒΡ«ζœΏMQ…®ΙΐΒΡ«χ”ρΒΡΟφΜΐΘΜ
(3)…η÷±œΏy=2x+9”κy÷αΫΜ”ΎΒψCΘ§”κ÷±œΏOMΫΜ”ΎΒψD(»γΆΦ2).œ÷ΫΪ≈ΉΈοœΏΤΫ“ΤΘ§±Θ≥÷ΕΞΒψ‘Ύ÷±œΏOD…œ.»τΤΫ“ΤΒΡ≈ΉΈοœΏ”κ…δœΏCD(Κ§ΕΥΒψC)ΟΜ”–ΙΪΙ≤Βψ ±Θ§ ‘ΧΫ«σΤδΕΞΒψΒΡΚαΉχ±ξhΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣA1ΓΔA2ΓΔΓ≠Γ≠ΓΔAnΓΔAnΘΪ1 «x÷α…œΒΡΒψΘ§«“OA1ΘΫA1A2ΘΫA2A3ΘΫΓ≠Γ≠ΘΫAnAnΘΪ1ΘΫ1Θ§Ζ÷±πΙΐΒψA1ΓΔA2ΓΔΓ≠Γ≠ΓΔAnΓΔAnΘΪ1Ήςx÷αΒΡ¥ΙœΏΫΜ÷±œΏyΘΫ2x”ΎΒψB1ΓΔB2ΓΔΓ≠Γ≠ΓΔBnΓΔBnΘΪ1Θ§Ν§Ϋ”A1B2ΓΔB1A2ΓΔA2B3ΓΔB2A3ΓΔΓ≠Γ≠ΓΔAnBnΘΪ1ΓΔBnAnΘΪ1Θ§“ά¥ΈœύΫΜ”ΎΒψP1ΓΔP2ΓΔP3ΓΔΓ≠Γ≠ΓΔPnΘ§ΓςA1B1P1ΓΔΓςA2B2P2ΓΔΓ≠Γ≠ΓΔΓςAnBnPnΒΡΟφΜΐ“ά¥ΈΈΣS1ΓΔS2ΓΔΓ≠Γ≠ΓΔSnΘ§‘ρSnΈΣ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏyΘΫax2+bx+3Ψ≠ΙΐΒψAΘ®©¹1Θ§0Θ©ΓΔBΘ®3Θ§0Θ©ΝΫΒψΘ§«“ΫΜy÷αΫΜ”ΎΒψCΘ°
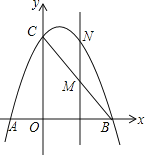
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΒψM «œΏΕΈBC…œΒΡΒψΘ®≤Μ”κBΓΔC÷ΊΚœΘ©Θ§ΙΐMΉςMNΓΈy÷αΫΜ≈ΉΈοœΏ”ΎNΘ§»τΒψMΒΡΚαΉχ±ξΈΣmΘ§«κ”ΟmΒΡ¥ζ ΐ Ϋ±μ ΨMNΒΡ≥ΛΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§Ν§Ϋ”NBΘ§NCΘ§ «Ζώ¥φ‘ΎΒψMΘ§ ΙΓςBNCΒΡΟφΜΐΉν¥σΘΩ»τ¥φ‘ΎΘ§«σmΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΓ―OΒΡΑκΨΕ «5Θ§AB «Γ―OΒΡœ“Θ§÷±ΨΕCDΓΆAB”ΎΒψEΘ°
Θ®1Θ©ΒψF «Γ―O…œ»Έ“β“ΜΒψΘ§«κΫω”ΟΈόΩΧΕ»ΒΡ÷±≥ΏΜ≠≥ωΓœAFBΒΡΫ«ΤΫΖ÷œΏΘΜ
Θ®2Θ©»τACΘΫ8Θ§ ‘«σABΒΡ≥ΛΘ°
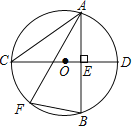
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ‘”Ύ“ΜΗωΚ· ΐΘ§Β±Ή‘±δΝΩx»Γn ±Θ§Κ· ΐ÷ΒyΒ»”Ύ4Θ≠nΘ§Έ“Ο«≥ΤnΈΣ’βΗωΚ· ΐΒΡΓΑΕΰΚœΒψΓ±Θ§»γΙϊΕΰ¥ΈΚ· ΐyΘΫmx2+x+1”–ΝΫΗωœύ“λΒΡΕΰΚœΒψx1Θ§x2Θ§«“x1ΘΦx2ΘΦ1Θ§‘ρmΒΡ»Γ÷ΒΖΕΈß «______Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏ![]() Ψ≠ΙΐΒψ
Ψ≠ΙΐΒψ![]() ΚΆΒψ
ΚΆΒψ![]() Θ§”κ
Θ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() .
.
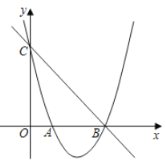
Θ®1Θ©«σ¥Υ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©»τΒψ![]() «÷±œΏ
«÷±œΏ![]() œ¬ΖΫΒΡ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ®≤ΜΒψ
œ¬ΖΫΒΡ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ®≤ΜΒψ![]() Θ§
Θ§![]() ÷ΊΚœΘ©Θ§ΙΐΒψ
÷ΊΚœΘ©Θ§ΙΐΒψ![]() Ής
Ής![]() ÷αΒΡΤΫ––œΏΫΜ÷±œΏ
÷αΒΡΤΫ––œΏΫΜ÷±œΏ![]() ”ΎΒψ
”ΎΒψ![]() Θ§…ηΒψ
Θ§…ηΒψ![]() ΒΡΚαΉχ±ξΈΣ
ΒΡΚαΉχ±ξΈΣ![]() .
.
ΔΌ”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ ΨœΏΕΈ
ΒΡ¥ζ ΐ Ϋ±μ ΨœΏΕΈ![]() ΒΡ≥ΛΘΜ
ΒΡ≥ΛΘΜ
ΔΎΝ§Ϋ”![]() Θ§
Θ§![]() Θ§«σ
Θ§«σ![]() ΒΡΟφΜΐΉν¥σ ±Βψ
ΒΡΟφΜΐΉν¥σ ±Βψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
Θ®3Θ©…η≈ΉΈοœΏΒΡΕ‘≥Τ÷α”κ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() «≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œ“ΜΒψΘ§
«≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œ“ΜΒψΘ§![]() ΈΣ
ΈΣ![]() ÷α…œ“ΜΒψΘ§ «Ζώ¥φ‘Ύ’β―υΒΡΒψ
÷α…œ“ΜΒψΘ§ «Ζώ¥φ‘Ύ’β―υΒΡΒψ![]() ΚΆΒψ
ΚΆΒψ![]() Θ§ ΙΒΟ“‘Βψ
Θ§ ΙΒΟ“‘Βψ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «Νβ–ΈΘΩ»γΙϊ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψ
ΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «Νβ–ΈΘΩ»γΙϊ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψ![]() ΒΡΉχ±ξΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡΉχ±ξΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com