
【题目】已知抛物线y=ax2+bx+3经过A(3,0),B(1,0)两点(如图1),顶点为M.
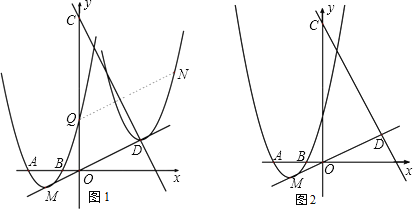
(1)a、b的值;
(2)设抛物线与y轴的交点为Q(如图1),直线y=2x+9与直线OM交于点D. 现将抛物线平移,保持顶点在直线OD上.当抛物线的顶点平移到D点时,Q点移至N点,求抛物线上的两点M、Q间所夹的曲线MQ扫过的区域的面积;
(3)设直线y=2x+9与y轴交于点C,与直线OM交于点D(如图2).现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)没有公共点时,试探求其顶点的横坐标h的取值范围.
【答案】(1)a=1,b=4;(2)MQ扫过的面积为![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)将A、B两点的坐标代入抛物线的解析式中,即可求出待定系数的值.
(2)连接MQ、DN后,由图可以发现曲线MQ扫过的面积正好是MQND的面积;连接QD,则MQND的面积是两倍的△MQD的面积,所以这道题实际求的是△MQD的面积;由(1)的抛物线解析式,不难求出顶点M的坐标,联立直线OM和直线CD的解析式可以求出点D的坐标;以OQ为底,M、D两点的横坐标差的绝对值为高即可得△MQD的面积,则此题可求.
(3)在平移过程中,抛物线的开口方向和大小是不变的,即二次项系数不变;抛物线的顶点始终在直线OM上,根据直线OM的解析式(y=![]() x)可表达出抛物线顶点的坐标(h,
x)可表达出抛物线顶点的坐标(h,![]() h),可据此先设出平移后的抛物线解析式;若求平移的抛物线与射线CD(含端点C)没有公共点时顶点横坐标的取值范围,那么就要考虑到两个关键位置:
h),可据此先设出平移后的抛物线解析式;若求平移的抛物线与射线CD(含端点C)没有公共点时顶点横坐标的取值范围,那么就要考虑到两个关键位置:
①抛物线对称轴右侧部分经过C点时,抛物线顶点横坐标h的值;
②抛物线对称轴左侧部分与直线CD恰好有且只有一个交点时,h的值;
解:(1)将A(-3,0),B(-1,0)代入抛物线y=ax2+bx+3中,得:
![]() ,
,
解得:a=1、b=4.
(2)连接MQ、QD、DN,
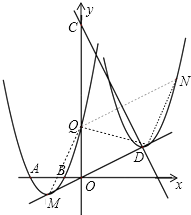
由图形平移的性质知:QN∥MD,即四边形MQND是平行四边形;
由(1)知,抛物线的解析式:y=x2+4x+3=(x+2)2-1,则点M(-2,-1),
当x=0时,y=3,
∴Q(0,3);
设直线OM的解析式为y=kx,
∴-2k=-1,
∴k=![]() ,
,
∴直线OM:y=![]() x,联立直线y=-2x+9,得:
x,联立直线y=-2x+9,得:
 ,
,
解得
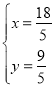 .
.
则D(![]() );
);
曲线QM扫过的区域的面积:S=S![]() MQND=2S△MQD
MQND=2S△MQD![]() ;
;
(3)由于抛物线的顶点始终在y=![]() x上,可设其坐标为(h,
x上,可设其坐标为(h,![]() h),设平移后的抛物线解析式为y=
h),设平移后的抛物线解析式为y=![]() h;
h;
①当平移后抛物线对称轴右侧部分经过点C(0,9)时,有:
h2+![]() h=9,解得:h=
h=9,解得:h=![]() (依题意,舍去正值)
(依题意,舍去正值)
②当平移后的抛物线与直线y=-2x+9只有一个交点时,依题意:
 ,
,
消去y,得:x2-(2h-2)x+h2+![]() h-9=0,
h-9=0,
则:△=(2h-2)2-4(h2+![]() h-9)=-10h+40=0,解得:h=4,
h-9)=-10h+40=0,解得:h=4,
结合图形,当平移的抛物线与射线CD(含端点C)没有公共点时,h<![]() 或h>4.
或h>4.


科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙,丙三个球迷决定通过抓阄来确定谁得到仅有的一张球票,他们准备了三张纸片,纸片上分别写上![]() ,然后将纸片折叠成外观一致的纸团,抓到
,然后将纸片折叠成外观一致的纸团,抓到![]() 纸片的人可以得到球票.
纸片的人可以得到球票.
(1)如果让甲从三张纸团中先抓一张,则甲一次就抓到写![]() 的纸片的概率为 (直接写出答案);
的纸片的概率为 (直接写出答案);
(2)抓阄前,乙产生了疑问:“谁先抓?先抓的人会不会抓中的机会比别人大?”你认为乙的怀疑有没有道理?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰梯形ABCD中,∠B=60°,P、Q同时从B出发,以每秒1个单位长度分别沿B→A→D→C和B→C→D方向运动至相遇时停止.设运动时间为t(秒),△BPQ的面积为S(平方单位),S与t的函数图象如图2,则下列结论错误的个数有( )
①当t=4秒时,S=![]() ;②AD=4;③当4≤t≤8时,S=
;②AD=4;③当4≤t≤8时,S=![]() ;④当t=9秒时,BP平分梯形ABCD的面积.
;④当t=9秒时,BP平分梯形ABCD的面积.
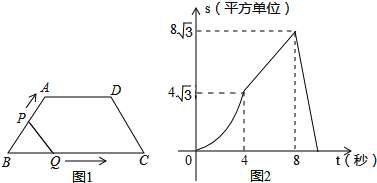
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.据统计,当每辆车的月租金为3000元时,可全部租出.每辆车的月租金每增加50元时,未租出的车将会增加1辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的租金定为多少元时,租赁公司的月收益(租金收入扣除维护费)可达到306600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
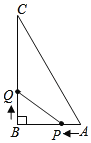
【题目】如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/秒的速度移动,同时点Q从B点开始沿BC边向点C以2cm/秒的速度移动,且当其中一点到达终点时,另一个点随之停止移动.
(1)P,Q两点出发几秒后,可使△PBQ的面积为8cm2.
(2)设P,Q两点同时出发移动的时间为t秒,△PBQ的面积为Scm2,请写出S与t的函数关系式,并求出△PBQ面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形OABC的边长为5,且tan∠AOC=![]() ,点E是线段BC的中点,过点A、E的抛物线y=ax2+bx+c与边AB交于点D.
,点E是线段BC的中点,过点A、E的抛物线y=ax2+bx+c与边AB交于点D.
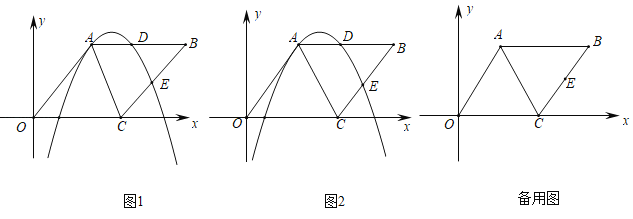
(1)求点A和点E的坐标;
(2)连结DE,将△BDE沿着DE翻折.
①当点B的对应点B'恰好落在线段AC上时,求点D的坐标;
②连接OB、BB',请直接写出此时该抛物线二次项系数a= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com