
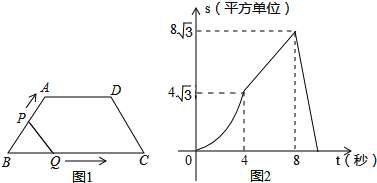
【题目】如图1,在等腰梯形ABCD中,∠B=60°,P、Q同时从B出发,以每秒1个单位长度分别沿B→A→D→C和B→C→D方向运动至相遇时停止.设运动时间为t(秒),△BPQ的面积为S(平方单位),S与t的函数图象如图2,则下列结论错误的个数有( )
①当t=4秒时,S=![]() ;②AD=4;③当4≤t≤8时,S=
;②AD=4;③当4≤t≤8时,S=![]() ;④当t=9秒时,BP平分梯形ABCD的面积.
;④当t=9秒时,BP平分梯形ABCD的面积.
A.1B.2C.3D.4
【答案】A
【解析】
先判断△BPQ为等边三角形,然后表示出△BPQ的面积可判断①;由图像可判断②;用待定系数法求出EF的解析式可判断③;设梯形高为h,分别表示出梯形的面积和△BCP的面积可判断④.
解:如图2所示,动点运动过程分为三个阶段:

(1)OE段,函数图象为抛物线,运动图形如图1-1所示.

此时点P在线段AB上、点Q在线段BC上运动.
∵BP=BQ=t,∠B=60°,
∴△BPQ为等边三角形,
作PH⊥BQ于H,
∵sinB=![]() ,
,
∴PH= ![]() t,
t,
∴S=![]() .
.
由函数图象可知,当t=4秒时,S=4![]() ,故选项①正确.
,故选项①正确.
(2)EF段,函数图象为直线,运动图形如图1-2所示.

此时点P在线段AD上、点Q在线段BC上运动.
由函数图象可知,此阶段运动时间为4s,
∴AD=1×4=4,故选项②正确.
设直线EF的解析式为:S=kt+b,将E(4,4![]() )、F(8,8
)、F(8,8![]() )代入得:
)代入得:
 ,
,
解得 ,
,
∴S=![]() t,故选项③错误.
t,故选项③错误.
(3)FG段,函数图象为直线,运动图形如图1-3所示.

此时点P、Q均在线段CD上运动.
设梯形高为h,则S梯形ABCD=![]() (AD+BC)h=
(AD+BC)h=![]() (4+8)h=6h;
(4+8)h=6h;
当t=9s时,DP=1,则CP=3,
∴CP:CD=3:4,
作DE⊥BC于E,PF⊥BC于F,则PF∥DE,
∴PF:DE=CP:CD=3:4,
∴PF=![]() ,
,
∴S△BCP=![]() S△BCD=
S△BCD=![]() 3h,
3h,
∴S△BCP=![]() S梯形ABCD,即BP平分梯形ABCD的面积,故选项④正确.
S梯形ABCD,即BP平分梯形ABCD的面积,故选项④正确.
故选:A.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
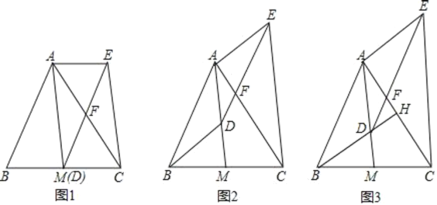
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM,连接AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM,求∠CAM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知Rt△AOB的两条直角边0A、08分别在y轴和x轴上,并且OA、OB的长分别是方程x2—7x+12=0的两根(OA<0B),动点P从点A开始在线段AO上以每秒l个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.
(1)求A、B两点的坐标。
(2)求当t为何值时,△APQ与△AOB相似,并直接写出此时点Q的坐标.
(3)当t=2时,在坐标平面内,是否存在点M,使以A、P、Q、M为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.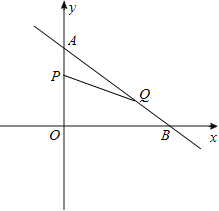
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步提高全民“节约用水”意识,某学校组织学生进行家庭月用水量情况调查活动,李明随机抽查了所住小区x户家庭的月用水量,绘制了下面不完整的统计图:

(1)求x并补全条形统计图;
(2)求这x户家庭的月平均用水量;并估计李明所住小区620户家庭中月用水量低于月平均用水量的家庭户数;
(3)从月用水量为5m3和9m3的家庭中任选两户进行用水情况问卷调查,求选出的两户中月用水量为5m3和9m3恰好各有一户家庭的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
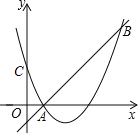
【题目】如图,二次函数y=(x﹣2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x﹣2)2+m的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3经过A(3,0),B(1,0)两点(如图1),顶点为M.
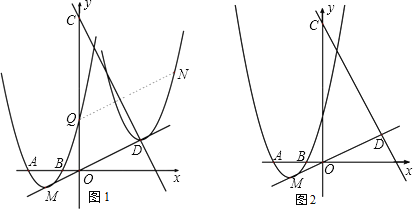
(1)a、b的值;
(2)设抛物线与y轴的交点为Q(如图1),直线y=2x+9与直线OM交于点D. 现将抛物线平移,保持顶点在直线OD上.当抛物线的顶点平移到D点时,Q点移至N点,求抛物线上的两点M、Q间所夹的曲线MQ扫过的区域的面积;
(3)设直线y=2x+9与y轴交于点C,与直线OM交于点D(如图2).现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)没有公共点时,试探求其顶点的横坐标h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1、A2、……、An、An+1是x轴上的点,且OA1=A1A2=A2A3=……=AnAn+1=1,分别过点A1、A2、……、An、An+1作x轴的垂线交直线y=2x于点B1、B2、……、Bn、Bn+1,连接A1B2、B1A2、A2B3、B2A3、……、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、……、Pn,△A1B1P1、△A2B2P2、……、△AnBnPn的面积依次为S1、S2、……、Sn,则Sn为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
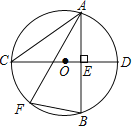
【题目】如图,已知⊙O的半径是5,AB是⊙O的弦,直径CD⊥AB于点E.
(1)点F是⊙O上任意一点,请仅用无刻度的直尺画出∠AFB的角平分线;
(2)若AC=8,试求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com