
【题目】如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径做圆,与BC相切于点C,过点A作AD⊥BO交BO的廷长线于点D,且∠AOD=∠BAD.

(1)求证:AB为⊙O的切线;
(2)若BC=6,tan∠ABC=![]() ,求AD的长.
,求AD的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据题意过O作OE⊥AB,再结合图形证明△BOC≌△BOE,从而证明OE=OC,便可证明AB为⊙O的切线.
(2)根据题意计算AB,AC的长度,进而计算OE的长度,在证明△ABD∽△OBC,利用相似比便可计算的AD的长.
解:(1)过点O作OE⊥AB于点E,
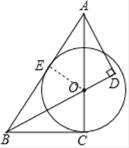
∵AD⊥BO于点D,
∴∠D=90°,
∴∠BAD+∠ABD=90°,∠AOD+∠OAD=90°,
∵∠AOD=∠BAD,
∴∠ABD=∠OAD,
又∵BC为⊙O的切线,
∴AC⊥BC,
∴∠BCO=∠D=90°,
∵∠BOC=∠AOD,
∴∠OBC=∠OAD=∠ABD,
在△BOC和△BOE中,
∵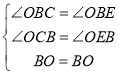
∴△BOC≌△BOE(AAS),
∴OE=OC,
∵OE⊥AB,
∴AB是⊙O的切线;
(2)∵∠ABC+∠BAC=90°,∠EOA+∠BAC=90°,
∴∠EOA=∠ABC,
∵tan∠ABC=![]() ,BC=6,
,BC=6,
∴AC=BCtan∠ABC=8,
则AB=10,
由(1)知BE=BC=6,
∴AE=4,
∵tan∠EOA=tan∠ABC=![]() ,
,
∴![]() ,
,
∴OE=3,OB=![]() ,
,
∵∠ABD=∠OBC,∠D=∠ACB=90°,
∴△ABD∽△OBC,
∴![]() ,即
,即![]() ,
,
∴AD=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系x O y中,△ABC 三个顶点坐标分别为A (1, 2),B(7,2),C(5,6).
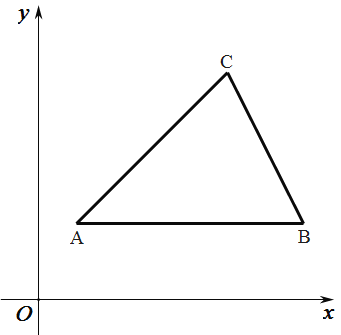
(1)在图中画出△ABC外接圆的圆心P;
(2)圆心P的坐标是______;
(3) tan∠ACB=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0)两点,且交y轴交于点C.
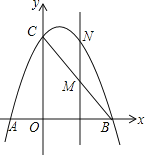
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B、C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点M,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,当自变量x取n时,函数值y等于4-n,我们称n为这个函数的“二合点”,如果二次函数y=mx2+x+1有两个相异的二合点x1,x2,且x1<x2<1,则m的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家政策的宏观调控下,某市的商品房的成交均价由2019年8月份的8000元/![]() 下降到2019年10月份的7500元/
下降到2019年10月份的7500元/![]() .
.
(1)求2019年9、10两月该市的商品房成交均价平均每月降价的百分率(精确到0.1,参考数据:![]() );
);
(2)如果房价继续回落,按(1)的降价的百分率,你认为到2019年12月份该市的商品房成交均价会跌破7000元/![]() 吗?请说明理由.
吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() ,
,![]() ,连接
,连接![]() .
.
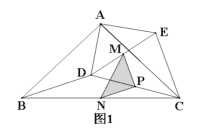

(1)如图1所示,线段![]() 与
与![]() 的数量关系是_____,位置关系是_____;
的数量关系是_____,位置关系是_____;
(2)在图1中,若点M、P、N分别为![]() 的中点,连接
的中点,连接![]() ,请判断
,请判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)如图2所示,若M、N、P分别为![]() 上的点,且满足
上的点,且满足![]() ,
,![]() ,连接
,连接![]() ,则线段
,则线段![]() 长度是多少?
长度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道A处开始,沿A﹣B﹣C路线对索道进行检修维护.如图:已知![]() 米,
米,![]() 米,AB与水平线
米,AB与水平线![]() 的夹角是
的夹角是![]() ,BC与水平线
,BC与水平线![]() 的夹角是
的夹角是![]() .求:本次检修中,检修人员上升的垂直高度
.求:本次检修中,检修人员上升的垂直高度![]() 是多少米?(结果精确到1米,参考数据:
是多少米?(结果精确到1米,参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在我国古建筑的大门上常常悬挂着巨大的匾额,图②中的线段BC就是悬挂在墙壁AM上的某块匾额的截面示意图.已知BC=1米,∠MBC=37°.从水平地面点D处看点C,仰角∠ADC=45°,从点E处看点B,仰角∠AEB=53°,且DE=2.4米,求匾额悬挂的高度AB的长.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ).
).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com