
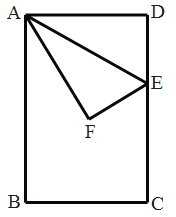
【题目】如图,在平面直角坐标系x O y中,△ABC 三个顶点坐标分别为A (1, 2),B(7,2),C(5,6).
(1)在图中画出△ABC外接圆的圆心P;
(2)圆心P的坐标是______;
(3) tan∠ACB=________.
【答案】(1)详见解析;(2)(4,3);(3)3
【解析】
(1)作AB,AC的中垂线,交于点P,即为所求点;
(2)由A (1, 2),B(7,2),可求出点P的横坐标,设点P的纵坐标为y,连接PA,PC,
由PA=PC,列出关于y的方程,即可求解;
(3)连接AP,BP,作△ABC外接圆,可得:∠ACB=∠APF,进而求出tan∠ACB的值.
(1)作AB,AC的中垂线,交于点P,即为所求点,如图所示:
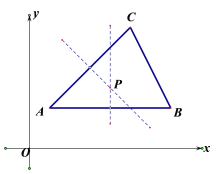
(2)∵A (1, 2),B(7,2),C(5,6),
∴点P的横坐标为(1+7)÷2=4,
设点P的纵坐标为y,连接PA,PC,如图1,
∵点P是△ABC外接圆的圆心,
∴PA=PC,
∴![]() ,解得:y=3,
,解得:y=3,
∴点P的坐标是:(4,3),
故答案是:(4,3).
(3)连接AP,BP,作△ABC外接圆,如图2,
∵∠ACB=![]() ∠APB,∠APF=
∠APB,∠APF=![]() ∠APB,
∠APB,
∴∠ACB=∠APF,
∴tan∠ACB= tan∠APF =![]() =
=![]() =3,
=3,
故答案是:3.

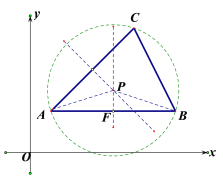
图1 图2


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
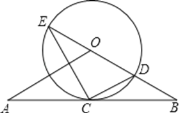
(1)求证:直线AB是⊙O的切线;
(2)试猜想BC,BD,BE三者之间的等量关系,并加以证明;
(3)若tan∠CED=![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市某景区经营一种新上市的纪念品,进价为20元/件,试营销阶段发现;当销售单价是30元时,每天的销售量为200件;销售单价每上涨2元,每天的销售量就减少10件.这种纪念品的销售单价为x(元).
(1)试确定日销售量y(台)与销售单价为x(元)之间的函数关系式;
(2)若要求每天的销售量不少于15件,且每件纪念品的利润至少为30元,则当销售单价定为多少时,该纪念品每天的销售利润最大,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙,丙三个球迷决定通过抓阄来确定谁得到仅有的一张球票,他们准备了三张纸片,纸片上分别写上![]() ,然后将纸片折叠成外观一致的纸团,抓到
,然后将纸片折叠成外观一致的纸团,抓到![]() 纸片的人可以得到球票.
纸片的人可以得到球票.
(1)如果让甲从三张纸团中先抓一张,则甲一次就抓到写![]() 的纸片的概率为 (直接写出答案);
的纸片的概率为 (直接写出答案);
(2)抓阄前,乙产生了疑问:“谁先抓?先抓的人会不会抓中的机会比别人大?”你认为乙的怀疑有没有道理?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=8,AD=6, 点E是边CD上一个动点,连接AE,将△AED沿直线AE翻折得△AEF.
(1) 当点C落在射线AF上时,求DE的长;
(2)以F为圆心,FB长为半径作圆F,当AD与圆F相切时,求cos∠FAB的值;
(3)若P为AB边上一点,当边CD上有且仅有一点Q满∠BQP=45°,直接写出线段BP长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.据统计,当每辆车的月租金为3000元时,可全部租出.每辆车的月租金每增加50元时,未租出的车将会增加1辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的租金定为多少元时,租赁公司的月收益(租金收入扣除维护费)可达到306600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径做圆,与BC相切于点C,过点A作AD⊥BO交BO的廷长线于点D,且∠AOD=∠BAD.

(1)求证:AB为⊙O的切线;
(2)若BC=6,tan∠ABC=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com