
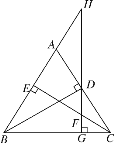
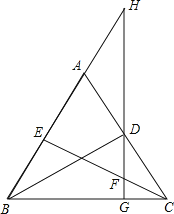
【题目】如图,BD,CE分别是△ABC的两边上的高,过D作DG⊥BC于G,分别交CE及BA的延长线于F,H,求证:
(1)DG2=BG·CG;
(2)BG·CG=GF·GH.
【答案】
【1】 证明:∵BD⊥AC,DG⊥BC,
∴![]()
∠DBC+∠DCG=∠GDC+∠DCG,
∴∠GDC=∠DBC,
∴![]()
∴BG:DG=DG:CG,
即![]()
【2】 同(1)中的方法,同理可证:△BGH∽△FGC,
∴BG:GF=GH:CG,
∴BGCG=GFGH.
【解析】
(1)根据题意结合图形,证明![]() 列出比例式,化为等积式即可解决问题.
列出比例式,化为等积式即可解决问题.
(2)方法同(1)中的解法,证明△BGH∽△FGC,列出比例式,化为等积式即可解决问题.
证明:(1)∵BD⊥AC,DG⊥BC,
∴![]()
∠DBC+∠DCG=∠GDC+∠DCG,
∴∠GDC=∠DBC,
∴![]()
∴BG:DG=DG:CG,
即![]()
(2)同(1)中的方法,同理可证:△BGH∽△FGC,
∴BG:GF=GH:CG,
∴BGCG=GFGH.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一块含30°角的直角三角板(如图),它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是( )
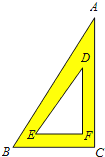
A、5cm B、6cm C、(6-![]() )cm D、(3+
)cm D、(3+![]() )cm
)cm
查看答案和解析>>
科目:初中数学 来源: 题型:
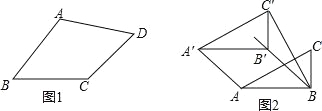
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)如图 1,在四边形 ABCD 中,添加一个条件使得四边形 ABCD 是“等邻边四边形”.请写出你添加的一个条件.
(2)小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由.
(3)如图 2,小红作了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,并将 Rt△ABC 沿∠ABC 的平分线 BB′方向平移得到△A′B′C′,连结 AA′, BC′.小红要使得平移后的四边形 ABC′A′是“等邻边四边形”,应平移多少距离(即线段 B′B 的长)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 先阅读下面的材料,再解答下面的问题:如果两个三角形的形状相同,则称这两个三角形相似.如图1,△ABC与△DEF形状相同,则称△ABC与△DEF相似,记作△ABC∽△DEF.那么,如何说明两个三角形相似呢?我们可以用“两角分别相等的三角形相似”加以说明.用数学语言表示为:
如图1:在△ABC与△DEF中,∵∠A=∠D,∠B=∠E,∴△ABC∽△DEF.
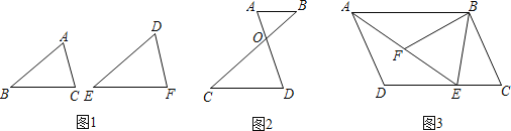
请你利用上述定理解决下面的问题:
(1)下列说法:①有一个角为50°的两个等腰三角形相似;②有一个角为100°的两个等腰三角形相似;③有一个锐角相等的两个直角三角形相似;④两个等边三角形相似.其中正确的是______(填序号);
(2)如图2,已知AB∥CD,AD与BC相交于点O,试说明△ABO∽△DCO;
(3)如图3,在平行四边形ABCD中,E是DC上一点,连接AE.F为AE上一点,且∠BFE=∠C,求证:△ABF∽△EAD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为
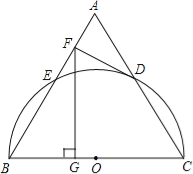
A. 4 B. ![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市政规划出一块矩形土地用于某项目开发,其中![]()
![]() ,设计分区如图所示,
,设计分区如图所示,![]() 为矩形内一点,作
为矩形内一点,作![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,
,![]() 过点
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,其中丙区域用于主建筑区,其余各区域均用于不同种类绿化.
,其中丙区域用于主建筑区,其余各区域均用于不同种类绿化.
![]() 若点
若点![]() 是
是![]() 的中点,求
的中点,求![]() 的长;
的长;
![]() 要求绿化占地面积不小于
要求绿化占地面积不小于![]() ,规定乙区域面积为
,规定乙区域面积为![]()
①若将甲区域设计成正方形形状,能否达到设计绿化要求?请说明理由;
②若主建筑丙区域不低于乙区域面积的![]() ,则
,则![]() 的最大值为
的最大值为 ![]() (请直接写出答案)
(请直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是____.
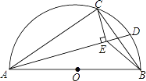
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O 的直径 AB 长为 10,弦 MN⊥AB,将⊙O 沿 MN 翻折,翻折后点 B 的对应点为点 B′,若 AB′=2,MB′的长为( )
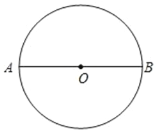
A. 2 ![]() B. 2
B. 2![]() 或 2
或 2![]() C. 2
C. 2![]() D. 2
D. 2 ![]() 或 2
或 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com