
【题目】 先阅读下面的材料,再解答下面的问题:如果两个三角形的形状相同,则称这两个三角形相似.如图1,△ABC与△DEF形状相同,则称△ABC与△DEF相似,记作△ABC∽△DEF.那么,如何说明两个三角形相似呢?我们可以用“两角分别相等的三角形相似”加以说明.用数学语言表示为:
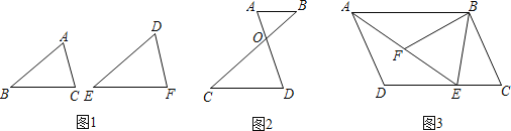
如图1:在△ABC与△DEF中,∵∠A=∠D,∠B=∠E,∴△ABC∽△DEF.
请你利用上述定理解决下面的问题:
(1)下列说法:①有一个角为50°的两个等腰三角形相似;②有一个角为100°的两个等腰三角形相似;③有一个锐角相等的两个直角三角形相似;④两个等边三角形相似.其中正确的是______(填序号);
(2)如图2,已知AB∥CD,AD与BC相交于点O,试说明△ABO∽△DCO;
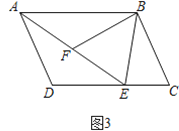
(3)如图3,在平行四边形ABCD中,E是DC上一点,连接AE.F为AE上一点,且∠BFE=∠C,求证:△ABF∽△EAD.
【答案】(1)②③④;(2)见解析;(3)见解析
【解析】
(1)由于50°的角可作为等腰三角形的顶角,也可以作为底角,由此可判断①;而100°的角只能作为等腰三角形的顶角,故可判断②;根据直角三角形的性质可判断③;根据等边三角形的性质可判断④,进而可得答案;
(2)根据平行线的性质和材料提供的方法解答即可;
(3)根据平行四边形的性质和平行线的性质可得∠BAE=∠AED,∠D+∠C=180°,然后根据已知和补角的性质可得∠D=∠AFB,进而可得结论.
解:(1)①由于50°的角可作为等腰三角形的顶角,也可以作为底角,所以有一个角为50°的两个等腰三角形不一定相似,所以①错误;
②由于100°的角只能作为等腰三角形的顶角,所以有一个角为100°的两个等腰三角形一定相似,所以②正确;
③有一个锐角相等的两个直角三角形一定相似,所以③正确;
④两个等边三角形一定相似,所以④正确.
故答案为②③④;
(2)∵AB∥CD,∴∠A=∠D,∠B=∠C,
∴△ABO∽△DCO;
(3)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠BAE=∠AED,∠D+∠C=180°,
∵∠AFB+∠BFE=180°,∠BFE=∠C,
∴∠D=∠AFB,
∴△ABF∽△EAD.


科目:初中数学 来源: 题型:
【题目】如图4所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
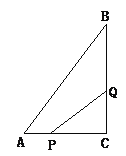
(1)、如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
(2)、点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
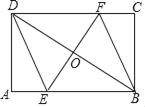
【题目】如图,在矩形ABCD中,AB=8,BC=4,过对角线BD的中点O的直线分别交AB、CD于点E、F,连接DE,BF.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:直线![]() 与直线
与直线![]() 互为“友好直线”,如:直线
互为“友好直线”,如:直线![]() 与
与![]() 互为“友好直线”.
互为“友好直线”.
(1)点![]() 在直线
在直线![]() 的“友好直线”上,则
的“友好直线”上,则![]() ________.
________.
(2)直线![]() 上的点
上的点![]() 又是它的“友好直线”上的点,求点
又是它的“友好直线”上的点,求点![]() 的坐标;
的坐标;
(3)对于直线![]() 上的任意一点
上的任意一点![]() ,都有点
,都有点![]() 在它的“友好直线”上,求直线
在它的“友好直线”上,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)把下面的证明补充完整
已知:如图,直线AB、CD被直线EF所截,AB∥CD,EG平分∠BEF,FG平分∠DFE,EG、FG交于点G.求证:EG⊥FG.

证明:∵AB∥CD(已知)
∴∠BEF+∠DFE=180°(______),
∵EG平分∠BEF,FG平分∠DFE(已知),
∴______,______(______),
∴∠GEF+∠GFE=![]() (∠BEF+∠DFE)(______),
(∠BEF+∠DFE)(______),
∴∠GEF+∠GFE=![]() ×180°=90°(______),
×180°=90°(______),
在△EGF中,∠GEF+∠GFE+∠G=180°(______),
∴∠G=180°-90°=90°(等式性质),
∴EG⊥FG(______).
(2)请用文字语言写出(1)所证命题:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
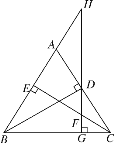
【题目】如图,BD,CE分别是△ABC的两边上的高,过D作DG⊥BC于G,分别交CE及BA的延长线于F,H,求证:
(1)DG2=BG·CG;
(2)BG·CG=GF·GH.
查看答案和解析>>
科目:初中数学 来源: 题型:
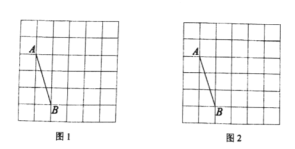
【题目】如图,在![]() 的方格纸中,每一个小正方形的边长均为
的方格纸中,每一个小正方形的边长均为![]() ,点
,点![]() 在格点上,用无刻度直尺按下列要求作图,保留必要的作图痕迹.
在格点上,用无刻度直尺按下列要求作图,保留必要的作图痕迹.
![]() 在图1中,以
在图1中,以![]() 为边画一个正方形
为边画一个正方形![]() ;
;
![]() 在图2中,以
在图2中,以![]() 为边画一个面积为
为边画一个面积为![]() 的矩形
的矩形![]() (
(![]() 可以不在格点上).
可以不在格点上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果生产基地,某天安排30名工人采摘枇杷或草莓(每名工人只能做其中一项工作),并且每人每天摘0.4吨枇杷或0.3吨草莓,当天的枇杷售价每吨2000元,草莓售价每吨3000元,设安排其中x名工人采摘枇杷,两种水果当天全部售出,销售总额达y元.
(1)求y与x之间的函数关系式;
(2)若要求当天采摘枇杷的数量不少于草莓的数量,求销售总额的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com