练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在的方格纸中，每一个小正方形的边长均为，点在格点上，用无刻度直尺按下列要求作图，保留必要的作图痕迹．

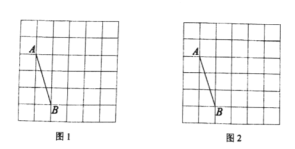
    在图1中，以为边画一个正方形；

    在图2中，以为边画一个面积为的矩形（可以不在格点上）．

    【答案】（1）详情见解析；（2）详情见解析

    【解析】

    （1）观察图中AB，可知AB为以三个方格组成的矩形的对角线，据此根据方格的特点结合矩形的性质及正方形的判定定理进一步画出图形即可；

    （2）首先根据题意按照（1）中作法画出正方形ABEF，结合题意可知其面积为10，据此，我们只要利用矩形对角线互相平分且相等的性质找到AF与BC的中点，然后连接起来即可得出答案.

    （1）如图1中，正方形ABCD即为所求：

    （2）如图2中，矩形ABCD即为所求：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°，顶部的仰角为37°，已知教学楼和实验楼在同一平面上，观测点距地面的垂直高度AB为15m，求实验楼的垂直高度即CD长（精确到1m）．

    参考值：sin37°=0.60，cos37°=0.80，tan37°=0.75．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）.

    (1) 请画出△ABC向左平移5个单位长度后得到的△ABC；

    (2) 请画出△ABC关于原点对称的△ABC；

    (3) 在轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 先阅读下面的材料，再解答下面的问题：如果两个三角形的形状相同，则称这两个三角形相似．如图1，△ABC与△DEF形状相同，则称△ABC与△DEF相似，记作△ABC∽△DEF．那么，如何说明两个三角形相似呢？我们可以用“两角分别相等的三角形相似”加以说明．用数学语言表示为：

    如图1：在△ABC与△DEF中，∵∠A=∠D，∠B=∠E，∴△ABC∽△DEF．

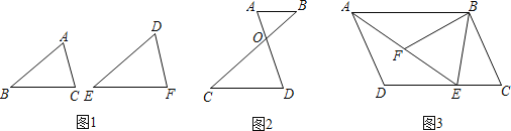
    请你利用上述定理解决下面的问题：

    （1）下列说法：①有一个角为50°的两个等腰三角形相似；②有一个角为100°的两个等腰三角形相似；③有一个锐角相等的两个直角三角形相似；④两个等边三角形相似．其中正确的是______（填序号）；

    （2）如图2，已知AB∥CD，AD与BC相交于点O，试说明△ABO∽△DCO；

    （3）如图3，在平行四边形ABCD中，E是DC上一点，连接AE．F为AE上一点，且∠BFE=∠C，求证：△ABF∽△EAD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

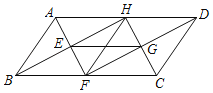
    【题目】已知：如图，ABCD中，∠BAD与∠ADC的角平分线交于BC边的点F，∠ABC与∠BCD的角平分线交于AD边的点H．

    （1）求证：四边形EFGH为矩形．

    （2）若HF＝3，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】市政规划出一块矩形土地用于某项目开发，其中，设计分区如图所示，为矩形内一点，作于点交于点，过点作交于点，其中丙区域用于主建筑区，其余各区域均用于不同种类绿化．

    若点是的中点，求的长；

    要求绿化占地面积不小于，规定乙区域面积为

    ①若将甲区域设计成正方形形状，能否达到设计绿化要求?请说明理由；

    ②若主建筑丙区域不低于乙区域面积的，则的最大值为 （请直接写出答案）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：

    （1）请在图中确定该圆弧所在圆心D点的位置，D点坐标为　 　；

    （2）连接AD、CD，求⊙D的半径及扇形DAC的圆心角度数；

    （3）若扇形DAC是某一个圆锥的侧面展开图，求该圆锥的底面半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】星马公司到某大学从应届毕业生中招聘公司职员，对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试成果认定，三项得分满分都为100分，三项的分数分别为 的比例计入每人的最后总分，有4位应聘者的得分如下所示：

    项目

    得分

    应聘者

    专业知识

    英语水平

    参加社会实践与社团活动等

    A

    85

    85

    90

    B

    85

    85

    70

    C

    80

    90

    70

    D

    80

    90

    50

    （1）写出4位应聘者的总分；

    （2）已知这4人专业知识、英语水平、参加社会实践与社团活动等三项的得分对应的方差分别为12.5、6.25、200，你对应聘者有何建议？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

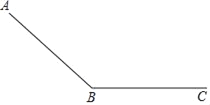
    【题目】如图，一个滑道由滑坡（AB段）和缓冲带（BC段）组成，滑雪者在滑坡上滑行的距离y1（单位：m）和滑行时间t1（单位s）满足二次函数关系，并测得相关数据：

    滑行时间t1/s

    0

    1

    2

    3

    4

    滑行距离y1/s

    0

    4.5

    14

    28.5

    48

    滑雪者在缓冲带上滑行的距离y2（单位：m）和滑行时间t2（单位：s）满足：y2=52t2﹣2t22，滑雪者从A出发在缓冲带BC上停止，一共用了23s．

    （1）求y1和t1满足的二次函数解析式；

    （2）求滑坡AB的长度．

    查看答案和解析>>

    同步练习册答案