
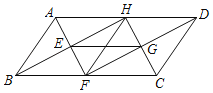
【题目】已知:如图,ABCD中,∠BAD与∠ADC的角平分线交于BC边的点F,∠ABC与∠BCD的角平分线交于AD边的点H.
(1)求证:四边形EFGH为矩形.
(2)若HF=3,求BC的长.
【答案】(1)详见解析;(2)6.
【解析】
(1)由平行四边形的性质可得∠BAD+∠ADC=180![]() ,∠ABC+∠BAD=180
,∠ABC+∠BAD=180![]() ,∠DAB+∠ABC=180
,∠DAB+∠ABC=180![]() ,由角平分线的性质可得∠AFD=90
,由角平分线的性质可得∠AFD=90![]() ,∠BHC=90
,∠BHC=90![]() ,∠AEB=∠FEH=90
,∠AEB=∠FEH=90![]() ,可证四边形EFGH为矩形;
,可证四边形EFGH为矩形;
(2)由矩形的性质可得EG=HF=3,通过证明EG是中位线,可得BC=2EG=6.
解:(1)∵四边形ABCD是平行四边形,
∴∠BAD+∠ADC=180![]() ,∠ABC+∠BAD=180
,∠ABC+∠BAD=180![]() ,∠DAB+∠ABC=180
,∠DAB+∠ABC=180![]()
∵∠BAD与∠ADC的角平分线交于BC边的点F,
∴∠BAF=∠DAF=![]() ∠BAD,∠ADF=
∠BAD,∠ADF=![]() ∠ADC,
∠ADC,
∴∠DAF+∠ADF=90![]() ,
,
∴∠AFD=90![]() ,
,
同理可证∠BHC=90![]() ,∠AEB=∠FEH=90
,∠AEB=∠FEH=90![]() ,
,
∴四边形EFGH是矩形;
(2)∵四边形EFGH为矩形.
∴EG=HF=3,
∵∠BAF=∠HAF,AE=AE,∠AEB=∠AEH=90![]() ,
,
∴△AEB≌△AEH(ASA)
∴BE=EH,
同理,HG=GC,
所以EG是△BHC的中位线
∴BC=2EG=6.


科目:初中数学 来源: 题型:
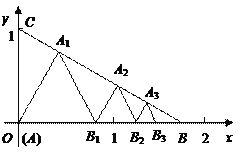
【题目】如图所示,已知:点A(0,0),B(![]() ,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第
,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第![]() 个等边三角形的边长等于__________.
个等边三角形的边长等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)根据要求,解答下列问题.
①方程![]() 的解为________________;
的解为________________;
②方程![]() 的解为________________;
的解为________________;
③方程![]() 的解为________________;
的解为________________;
(2)根据以上方程特征及其解的特征,请猜想:
①方程![]() 的解为________________;
的解为________________;
②关于![]() 的方程________________的解为
的方程________________的解为![]() ,
,![]() .
.
(3)请用配方法解方程![]() ,以验证猜想结论的正确性.
,以验证猜想结论的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)把下面的证明补充完整
已知:如图,直线AB、CD被直线EF所截,AB∥CD,EG平分∠BEF,FG平分∠DFE,EG、FG交于点G.求证:EG⊥FG.

证明:∵AB∥CD(已知)
∴∠BEF+∠DFE=180°(______),
∵EG平分∠BEF,FG平分∠DFE(已知),
∴______,______(______),
∴∠GEF+∠GFE=![]() (∠BEF+∠DFE)(______),
(∠BEF+∠DFE)(______),
∴∠GEF+∠GFE=![]() ×180°=90°(______),
×180°=90°(______),
在△EGF中,∠GEF+∠GFE+∠G=180°(______),
∴∠G=180°-90°=90°(等式性质),
∴EG⊥FG(______).
(2)请用文字语言写出(1)所证命题:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知,反比例函数y=![]() 的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
(1)求这个一次函数的表达式;
(2)若点P(m,n)在反比例函数图象上,且点P关于x轴对称的点Q恰好落在一次函数的图象上,求m2+n2的值;
(3)若M(x1,y1),N(x2,y2)是反比例函数在第一象限图象上的两点,满足x2-x1=2,y1+y2=3,求△MON的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
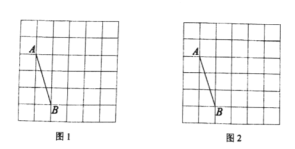
【题目】如图,在![]() 的方格纸中,每一个小正方形的边长均为
的方格纸中,每一个小正方形的边长均为![]() ,点
,点![]() 在格点上,用无刻度直尺按下列要求作图,保留必要的作图痕迹.
在格点上,用无刻度直尺按下列要求作图,保留必要的作图痕迹.
![]() 在图1中,以
在图1中,以![]() 为边画一个正方形
为边画一个正方形![]() ;
;
![]() 在图2中,以
在图2中,以![]() 为边画一个面积为
为边画一个面积为![]() 的矩形
的矩形![]() (
(![]() 可以不在格点上).
可以不在格点上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如右表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是________环,乙的平均成绩是________环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
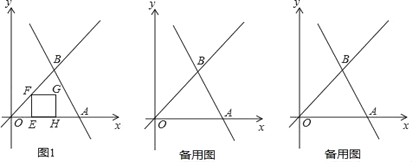
【题目】如图1,直线y=﹣2x+3与x轴交于点A,与直线y=x交于点B.
(1)点A坐标为 ,∠AOB= ;
(2)求S△OAB的值;
(3)动点E从原点O出发,以每秒1个单位长度的速度沿着O→A的路线向终点A匀速运动,过点E作EF⊥x轴交直线y=x于点F,再以EF为边向右作正方形EFGH.设运动t秒时,正方形EFGH与△OAB重叠部分的面积为S.求:S与t之间的函数关系式,并写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
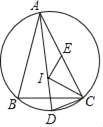
【题目】点I为△ABC的内心,连AI交△ABC的外接圆于点D,若AI=2CD,点E为弦AC的中点,连接EI,IC,若IC=6,ID=5,则IE的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com