
【题目】 已知,反比例函数y=![]() 的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
(1)求这个一次函数的表达式;
(2)若点P(m,n)在反比例函数图象上,且点P关于x轴对称的点Q恰好落在一次函数的图象上,求m2+n2的值;
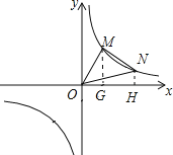
(3)若M(x1,y1),N(x2,y2)是反比例函数在第一象限图象上的两点,满足x2-x1=2,y1+y2=3,求△MON的面积.
【答案】(1)y=-x-3;(2)m2+n2=13;(3)S△MON=3
【解析】
(1)先求得A、B的坐标,然后根据待定系数法求解即可;
(2)由点P与点Q关于x轴对称可得点Q的坐标,然后根据图象上点的坐标特征可求得mn=2,n=m+3,然后代入所求式子整理化简即得结果;
(3)如图,过M作MG⊥x轴于G,过N作NH⊥x轴于H,根据反比例函数系数k的几何意义,利用S△MON=S梯形MNHG+S△MOG-S△NOH=S梯形MNHG即可求得结果.
解:(1)∵反比例函数y=![]() 的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1,
的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1,
∴A(﹣1,﹣2),B(﹣2,﹣1),
设一次函数的表达式为y=kx+b,把A(﹣1,﹣2),B(﹣2,﹣1)代入,得:
![]() ,解得
,解得![]() ,
,
∴这个一次函数的表达式为y=﹣x﹣3;
(2)∵点P(m,n)与点Q关于x轴对称,∴Q(m,-n),
∵点P(m,n)在反比例函数图象上,∴mn=2,
∵点Q恰好落在一次函数的图象上,∴﹣n=﹣m﹣3,即n=m+3,
∴m(m+3)=2,∴m2+3m=2,
∴m2+n2=m2+(m+3)2=2m2+6m+9=2(m2+3m)+9=2×2+9=13;
(3)如图,过M作MG⊥x轴于G,过N作NH⊥x轴于H,
∵M(x1,y1),N(x2,y2)是反比例函数y=![]() 在第一象限图象上的两点,
在第一象限图象上的两点,
∴S△MOG=S△NOH=![]() =1,
=1,
∵x2-x1=2,y1+y2=3,
∴S△MON=S梯形MNHG+S△MOG-S△NOH=S梯形MNHG=![]() =
=![]() =3.
=3.


科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元。
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
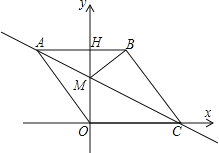
【题目】如图,在平面直角坐标系中,点![]() 是坐标原点,四边形
是坐标原点,四边形![]() 是菱形,点
是菱形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]() ,连接
,连接![]()
(1)菱形![]() 的边长是________;
的边长是________;
(2)求直线![]() 的解析式;
的解析式;
(3)动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 以2个单位长度/秒的速度向终点
以2个单位长度/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒,求
秒,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共50棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树的总金额为56000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
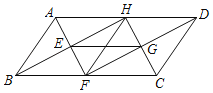
【题目】已知:如图,ABCD中,∠BAD与∠ADC的角平分线交于BC边的点F,∠ABC与∠BCD的角平分线交于AD边的点H.
(1)求证:四边形EFGH为矩形.
(2)若HF=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
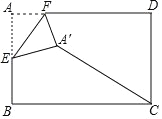
【题目】如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若圆的一条弦把圆分成度数比为1:4的两段弧,则弦所对的圆周角等于( )
A. 36° B. 72° C. 36°或144° D. 72°或108°
查看答案和解析>>
科目:初中数学 来源: 题型:
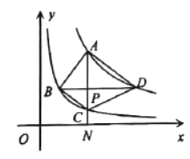
【题目】如图,四边形![]() 在平面直角坐标系的第一象限内,其四个顶点分别在反比例函数
在平面直角坐标系的第一象限内,其四个顶点分别在反比例函数![]() 与
与![]() 的图象上,对角线
的图象上,对角线![]() 于点
于点![]() ,
,![]() 轴于点
轴于点![]() .
.
(1)若![]() ,试求
,试求![]() 的值;
的值;
(2)当![]() ,点
,点![]() 是线段
是线段![]() 的中点时,试判断四边形
的中点时,试判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
(3)直线![]() 与
与![]() 轴相交于
轴相交于![]() 点.当四边形
点.当四边形![]() 为正方形时,请求出
为正方形时,请求出![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com