
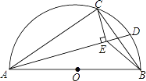
【题目】如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是____.
【答案】![]() ﹣2≤BE<3
﹣2≤BE<3
【解析】
由∠AEC=90°知E在以AC为直径的⊙M的![]() 上(不含点C、可含点N),从而得BE最短时,即为连接BM与⊙M的交点(图中点E′点),在Rt△BCM中利用勾股定理求得BM=
上(不含点C、可含点N),从而得BE最短时,即为连接BM与⊙M的交点(图中点E′点),在Rt△BCM中利用勾股定理求得BM=![]() ,从而得BE长度的最小值BE′=BM-ME′=
,从而得BE长度的最小值BE′=BM-ME′=![]() -2;由BE最长时即E与C重合,根据BC=3且点E与点C不重合,得BE<3,从而得出答案.
-2;由BE最长时即E与C重合,根据BC=3且点E与点C不重合,得BE<3,从而得出答案.
如图,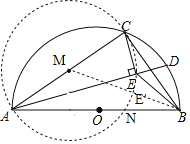
由题意知,∠AEC=90°,
∴E在以AC为直径的⊙M的![]()
上(不含点C、可含点N),
∴BE最短时,即为连接BM与⊙M的交点(图中点E′点),
∵AB=5,AC=4,
∴BC=3,CM=2,
则BM=![]() =
=![]() =
=![]() ,
,
∴BE长度的最小值BE′=BM-ME′=![]() -2,
-2,
BE最长时,即E与C重合,
∵BC=3,且点E与点C不重合,
∴BE<3,
所以![]() -2≤BE<3.
-2≤BE<3.
故答案是:![]() -2≤BE<3.
-2≤BE<3.


科目:初中数学 来源: 题型:
【题目】某贮水塔在工作期间,每小时的进水量和出水量都是固定不变的.从凌晨4点到早8点只进水不出水,8点到12点既进水又出水,14点到次日凌晨只出水不进水.下图是某日水塔中贮水量y(立方米)与x(时)的函数图象.
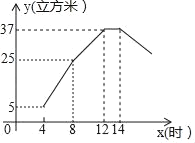
(1)求每小时的进水量;
(2)当8≤x≤12时,求y与x之间的函数关系式;
(3)从该日凌晨4点到次日凌晨,当水塔中的贮水量不小于28立方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
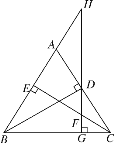
【题目】如图,BD,CE分别是△ABC的两边上的高,过D作DG⊥BC于G,分别交CE及BA的延长线于F,H,求证:
(1)DG2=BG·CG;
(2)BG·CG=GF·GH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果生产基地,某天安排30名工人采摘枇杷或草莓(每名工人只能做其中一项工作),并且每人每天摘0.4吨枇杷或0.3吨草莓,当天的枇杷售价每吨2000元,草莓售价每吨3000元,设安排其中x名工人采摘枇杷,两种水果当天全部售出,销售总额达y元.
(1)求y与x之间的函数关系式;
(2)若要求当天采摘枇杷的数量不少于草莓的数量,求销售总额的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
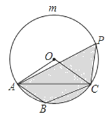
【题目】如图,在△ABC中,∠ABC=120°,⊙O是△ABC的外接圆,点P是![]() 上的一个动点.
上的一个动点.
(1)求∠AOC的度数;
(2)若⊙O的半径为2,设点P到直线AC的距离为x,图中阴影部分的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围.\
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 某种彩票中奖的概率是![]() ,买1000张该种彩票一定会中奖
,买1000张该种彩票一定会中奖
B. 了解一批电视机的使用寿命适合用抽样调查
C. 若甲组数据的标准差S甲=0.31,乙组数据的标准差S乙=0.25,则乙组数据比甲组数据稳定
D. 在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
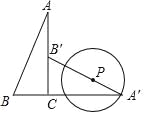
【题目】如图,△ABC中,∠ACB=90°,tanA=![]() ,AB=13,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B′上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为_____.
,AB=13,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B′上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com