
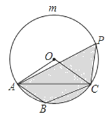
【题目】如图,在△ABC中,∠ABC=120°,⊙O是△ABC的外接圆,点P是![]() 上的一个动点.
上的一个动点.
(1)求∠AOC的度数;
(2)若⊙O的半径为2,设点P到直线AC的距离为x,图中阴影部分的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围.\
【答案】(1)120°;(2)y=![]() ﹣
﹣![]() +
+![]() x(0≤x≤3)
x(0≤x≤3)
【解析】
(1)先根据圆内接四边形的性质求出∠P的度数,再由圆周角定理即可得出结论;
(2)过点O作OH⊥AC于H,根据锐角三角函数的定义得出AH及OH的长,进而得出AC的长,用x表示出△APC的面积,再根据y=S扇形AOC-S△AOC+S△APC即可得出结论.
解:(1)∵∠ABC=120°,四边形ABCP是圆内接四边形,
∴∠P=180°﹣120°=60°,
∴∠AOC=2∠APC=120°;
(2)过点O作OH⊥AC于H,
∵∠AOC=120°,OC=OA=2,
∴∠OAC=30°,
∴AH=OAcos30°=2×![]() =
=![]() ,OH=
,OH=![]() OA=1,
OA=1,
∴AC=2AH=2![]() ,
,
∴S△APC=![]() ACx=
ACx=![]() x,
x,
∴y=S扇形AOC﹣S△AOC+S△APC=![]() ﹣
﹣![]() ×2
×2![]() ×1+
×1+![]() x=
x=![]() ﹣
﹣![]() +
+![]() x(0≤x≤3).
x(0≤x≤3).


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
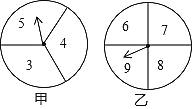
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后, 若指针所指区域内两数和等于 12,则李燕获胜;若指针所指区域内两数和等于 13,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)游戏对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为
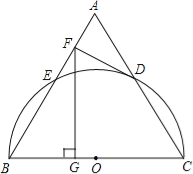
A. 4 B. ![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
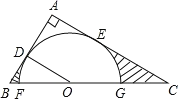
【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=![]() .
.
(1)求证:AE是 O的切线;
(2)求图中两部分阴影面积的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
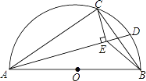
【题目】如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
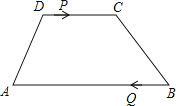
【题目】如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市开展“环境治理留住青山绿水,绿色发展赢得金山银山”活动,对其周边的环境污染进行综合治理.![]() 年对
年对![]() 、
、![]() 两区的空气量进行监测,将当月每天的空气污染指数(简称:
两区的空气量进行监测,将当月每天的空气污染指数(简称:![]() )的平均值作为每个月的空气污染指数,并将
)的平均值作为每个月的空气污染指数,并将![]() 年空气污染指数绘制如下表.据了解,空气污染指数
年空气污染指数绘制如下表.据了解,空气污染指数![]() 时,空气质量为优:
时,空气质量为优:![]() 空气污染指数
空气污染指数![]() 时,空气质量为良:
时,空气质量为良:![]() 空气污染指数
空气污染指数![]() 时,空气质量为轻微污染.
时,空气质量为轻微污染.
月份 地区 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请求出![]() 、
、![]() 两区的空气污染指数的平均数;
两区的空气污染指数的平均数;
(2)请从平均数、众数、中位数、方差等统计量中选两个对![]() 区、
区、![]() 区的空气质量进行有效对比,说明哪一个地区的环境状况较好.
区的空气质量进行有效对比,说明哪一个地区的环境状况较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
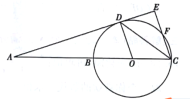
【题目】如图,点D是⊙O上一点,直线AE经过点D,直线AB经过圆心O,交⊙O于B,C两点,CE⊥AE,垂足为点E,交⊙O于点F,∠BCD=∠DCF
(1)求∠A+∠BOD的度数;
(2)若sin∠DCE=![]() ,⊙O的半径为5,求线段AB的长.
,⊙O的半径为5,求线段AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com