
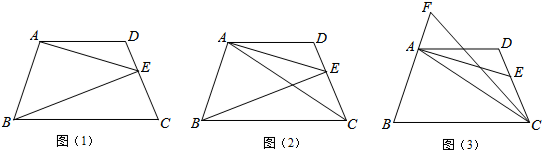
分析 (1)过E作EF∥AD,根据AD∥BC可得出EF∥BC,故可得出∠DAE=∠EAF,∠CBE=∠BEF,由此可得出结论;
(2)①根据AD∥BC可知∠DAC=∠ACB.再由AE平分∠DAC得出∠EAC=$\frac{1}{2}$∠DAC=$\frac{1}{2}$∠ACB,根据∠ABC=∠BAC,∠ABC+∠BAC+∠ACB=180°即可得出结论;
②由①知∠BAE=90°,故∠FAE=90°.再由三角形外角的性质得出∠AGC=90°+60°=150°.根据三角形内角和定理得出∠GAC+∠ACG=30°.由AE平分∠DAC,CF平分∠ACD及三角形内角和定理得出∠D的度数,再由平行线的性质即可得出结论.
解答 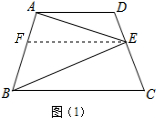 解:(1)过E作EF∥AD,
解:(1)过E作EF∥AD,
∵AD∥BC,
∴EF∥BC,
∴∠DAE=∠AEF,∠CBE=∠BEF,
∴∠AEB=∠DAE+∠CBE;
(2)①证明:∵AD∥BC,
∴∠DAC=∠ACB.
∵AE平分∠DAC,
∴∠EAC=$\frac{1}{2}$∠DAC=$\frac{1}{2}$∠ACB,
∵∠ABC=∠BAC,∠ABC+∠BAC+∠ACB=180°,
∴∠BAC+∠EAC=90°,
∴∠ABE+∠AEB=90°;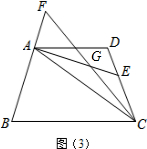 ②解:如图(3),由①知∠BAE=90°,
②解:如图(3),由①知∠BAE=90°,
∴∠FAE=90°.
∵∠F=60°,
∴∠AGC=90°+60°=150°.
∴∠GAC+∠ACG=30°.
∵AE平分∠DAC,CF平分∠ACD,
∴∠DAC+∠ACD=2(∠GAC+∠ACG)=60°,
∴∠D=180°-60°=120°.
∵AD∥BC,
∴∠BCD=180°-∠D=180°-120°=60°.
点评 本题考查的是平行线的性质,涉及到角平分线的性质、三角形内角和定理等知识,难度适中.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
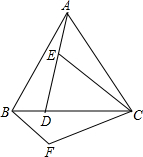 如图,已知△ABC是正三角形,点D是边BC上一点,连接AD,点E是线段AD上一点,连接CE,点F是△ABC外一点,∠CAD=∠CBF,连接BF和CF.
如图,已知△ABC是正三角形,点D是边BC上一点,连接AD,点E是线段AD上一点,连接CE,点F是△ABC外一点,∠CAD=∠CBF,连接BF和CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
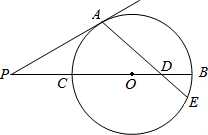 已知,如图,PA是⊙O切线,切点为A,PB交⊙O于C且过圆心O,D是OB中点,连结AB并延长交⊙O于E,若∠APB=30°,AP=$\sqrt{6}$,求AE的长.
已知,如图,PA是⊙O切线,切点为A,PB交⊙O于C且过圆心O,D是OB中点,连结AB并延长交⊙O于E,若∠APB=30°,AP=$\sqrt{6}$,求AE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 下图是由14个每相邻两点之间距离为1的点组成的“工”字形图形,请仅用无刻度的直尺通过连接图中的点,根据要求画图.
下图是由14个每相邻两点之间距离为1的点组成的“工”字形图形,请仅用无刻度的直尺通过连接图中的点,根据要求画图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
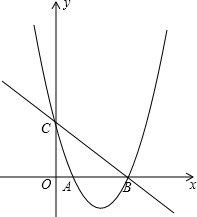 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,与y轴相交于点C,直线y=kx+n(k≠0)经过B,C两点,已知A(1,0),C(0,3),且BC=5.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,与y轴相交于点C,直线y=kx+n(k≠0)经过B,C两点,已知A(1,0),C(0,3),且BC=5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
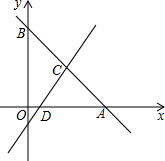 如图,在平面直角坐标系中,直线y=-x+8分别交两轴于点A、B,点C为线段AB的中点,点D在线段OA上,且CD的长是方程$\frac{2}{x+1}=\frac{1}{x-2}$的根.
如图,在平面直角坐标系中,直线y=-x+8分别交两轴于点A、B,点C为线段AB的中点,点D在线段OA上,且CD的长是方程$\frac{2}{x+1}=\frac{1}{x-2}$的根.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
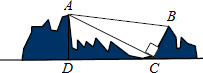 如图,某景区有一出索道游览山谷的旅游点,已知索道两端距离AB为1300米,在山脚C点测得BC的距离为500米,∠ACB=90°,在C点观测山峰顶点A的仰角∠ACD=23.5°,求山峰顶点A到C点的水平面高度AD.(参考数据:sin23.5°≈0.40,cos23.5°=0.92,tan23.5°=0.43)
如图,某景区有一出索道游览山谷的旅游点,已知索道两端距离AB为1300米,在山脚C点测得BC的距离为500米,∠ACB=90°,在C点观测山峰顶点A的仰角∠ACD=23.5°,求山峰顶点A到C点的水平面高度AD.(参考数据:sin23.5°≈0.40,cos23.5°=0.92,tan23.5°=0.43)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com