
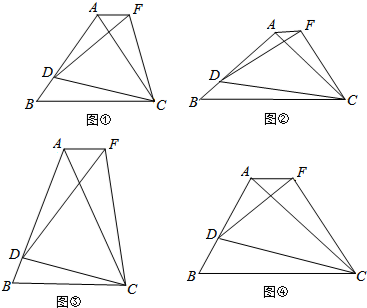
分析 (1)根据等边三角形的性质证明△FCA≌△DCB,得到线段AF与BD之间的数量关系;
(2)根据等腰直角三角形的性质证明△FCA∽△DCB,得到线段AF与BD之间的数量关系;
(3)Ⅰ、根据等腰三角形的性质和锐角三角函数的概念求出BC与AC的比,证明△BCD∽△ACF,得到线段AF与BD之间的数量关系;
Ⅱ、根据△FDC∽△ABC,证明△BCD∽△ACF,得到线段AF与BD之间的数量关系.
解答 解:(1)∵等边△ABC,等边△DCF,
∴FC=DC,AC=BC,∠FCA+∠ACD=∠BCD+∠ACD=60°,
∴∠FCA=∠DCB,
在△FCA和△DCB中,
$\left\{\begin{array}{l}{CF=CD}\\{∠FCA=∠DCB}\\{CA=CB}\end{array}\right.$,
∴△FCA≌△DCB,
∴BD=AF;
(2)∵(1)∵△ABC是等腰直角三角形,△DCF是等腰直角三角形,
∴$\frac{FC}{CD}$=$\frac{\sqrt{2}}{2}$,$\frac{AC}{CB}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{FC}{CD}$=$\frac{AC}{CB}$,
∠FCA+∠ACD=∠BCD+∠ACD=45°,
∴∠FCA=∠DCB,
∴△FCA∽△DCB,
∴$\frac{AF}{BD}$=$\frac{\sqrt{2}}{2}$;
(3)Ⅰ.∵△ABC为以BC为底边的等腰三角形,△FDC 为以DC为底边的等腰三角形,
∠BCA=∠DCF,
∴△ABC∽△FDC,
∴$\frac{CD}{CF}$=$\frac{BC}{AC}$,∠ACF=∠BCD,
∴△BCD∽△ACF,
∴$\frac{BD}{AF}$=$\frac{BC}{AC}$,
如图③,作AP⊥BC,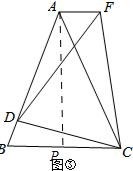
$\frac{BC}{AC}$=$\frac{2CP}{AC}$=2sin$\frac{1}{2}$∠BAC=2sin$\frac{1}{2}$α,
∴$\frac{BD}{AF}$=2sin$\frac{1}{2}$α;
Ⅱ、∵△FDC∽△ABC,
∴$\frac{CF}{CA}=\frac{CD}{CB}$,∠FCA+∠ACD=∠BCD+∠ACD,
∴∠FCA=∠DCB,
∴△FCA∽△DCB,
∴$\frac{BD}{AF}$=$\frac{BC}{AC}$=k.
点评 本题考查的是等边三角形、等腰三角形、等腰直角三角形的性质和全等三角形、相似三角形的判定和性质以及锐角三角函数的知识,正确运用类比思想、灵活运用所学的性质定理是解题的关键.


科目:初中数学 来源: 题型:解答题
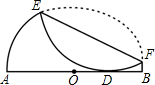 已知半圆O的直径AB=4,沿它的一条弦折叠.
已知半圆O的直径AB=4,沿它的一条弦折叠.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
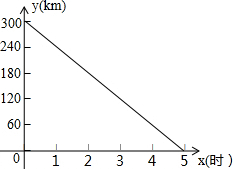 某货运公司甲乙两辆汽车,分别从AB两地同时以相同的速度发车,驾车驶往B城,乙车驶往A城,甲车与B城的距离y甲(km)与行驶时间x(时)的关系如图.
某货运公司甲乙两辆汽车,分别从AB两地同时以相同的速度发车,驾车驶往B城,乙车驶往A城,甲车与B城的距离y甲(km)与行驶时间x(时)的关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com