
| A. | m(m2-9) | B. | m(m-3)2 | C. | m(m+3)(m-3) | D. | m(m+9)(m-9) |
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:填空题
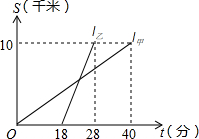 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲,l乙分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象.请你写出一个正确的说法:如答案不唯一,如①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了10分钟就到达培训中心;等..
甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲,l乙分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象.请你写出一个正确的说法:如答案不唯一,如①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了10分钟就到达培训中心;等..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
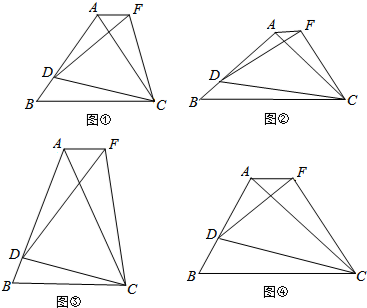
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}-\sqrt{2}$=1 | B. | a6÷a2=a3 | C. | x2+x3=x5 | D. | (-x2)3=-x6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
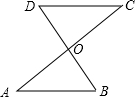 已知:如图,AC和BD相交于点O,OA=OC,OB=OD.
已知:如图,AC和BD相交于点O,OA=OC,OB=OD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
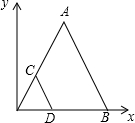 如图,把△COD扩大后得到△AOB,若点C,D,B的坐标分别为C(1,2),D(2,0),B(5,0).则点A的坐标为( )
如图,把△COD扩大后得到△AOB,若点C,D,B的坐标分别为C(1,2),D(2,0),B(5,0).则点A的坐标为( )| A. | (2,5) | B. | (2.5,5) | C. | (2,5) | D. | (3,6) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
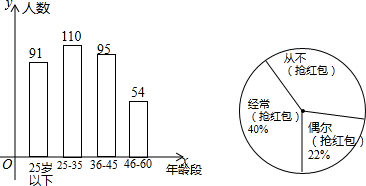
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
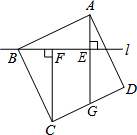 如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com