
分析 根据A(-2,m),B(5,n)两点在反比例函数$y=\frac{k}{x}$的图象上,求出m、n的值,用待定系数法求出a、b的值,计算得到答案.
解答 解:∵A(-2,m),B(5,n)两点在反比例函数$y=\frac{k}{x}$的图象上,
∴m=-$\frac{k}{2}$,n=$\frac{k}{5}$,
$\left\{\begin{array}{l}{-2a+b=-\frac{k}{2}}\\{5a+b=\frac{k}{5}}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=\frac{k}{10}}\\{b=-\frac{3k}{10}}\end{array}\right.$,
3a+b=0,
故答案为:0.
点评 本题考查的是反比例函数与一次函数的交点问题,根据运用待定系数法求出一次函数的系数是解题的关键,注意含有参数的二元一次方程组的解法.


科目:初中数学 来源: 题型:填空题
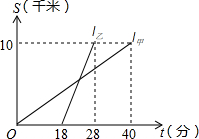 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲,l乙分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象.请你写出一个正确的说法:如答案不唯一,如①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了10分钟就到达培训中心;等..
甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲,l乙分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象.请你写出一个正确的说法:如答案不唯一,如①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了10分钟就到达培训中心;等..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知线段AB=a,在线段AB上有一点C,若AC=$\frac{3-\sqrt{5}}{2}$a,则点C是线段AB的黄金分割点吗?为什么?
已知线段AB=a,在线段AB上有一点C,若AC=$\frac{3-\sqrt{5}}{2}$a,则点C是线段AB的黄金分割点吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
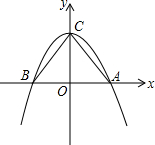 如图,抛物线y=-$\frac{1}{2}$x2+2与x轴交于A、B两点,其中点A在x轴的正半轴上,点B在x轴的负半轴上
如图,抛物线y=-$\frac{1}{2}$x2+2与x轴交于A、B两点,其中点A在x轴的正半轴上,点B在x轴的负半轴上查看答案和解析>>
科目:初中数学 来源: 题型:解答题
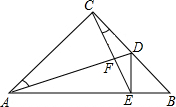 如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD是BC上的中线,CE⊥AD于F,交AB于E,连结DE,问∠CDA与∠BDE相等吗?为什么?
如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD是BC上的中线,CE⊥AD于F,交AB于E,连结DE,问∠CDA与∠BDE相等吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
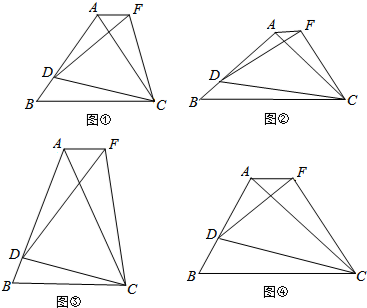
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}-\sqrt{2}$=1 | B. | a6÷a2=a3 | C. | x2+x3=x5 | D. | (-x2)3=-x6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com