
 已知线段AB=a,在线段AB上有一点C,若AC=$\frac{3-\sqrt{5}}{2}$a,则点C是线段AB的黄金分割点吗?为什么?
已知线段AB=a,在线段AB上有一点C,若AC=$\frac{3-\sqrt{5}}{2}$a,则点C是线段AB的黄金分割点吗?为什么? 分析 由已知求出线段BC与线段AB的比值,根据黄金比为$\frac{\sqrt{5}-1}{2}$进行解答即可得到答案.
解答 解:点C是线段AB的黄金分割点,
∵AB=a,AC=$\frac{3-\sqrt{5}}{2}$a,
∴BC=a-$\frac{3-\sqrt{5}}{2}$a=$\frac{\sqrt{5}-1}{2}$a,
则$\frac{BC}{AB}$=$\frac{\sqrt{5}-1}{2}$,
则点C是线段AB的黄金分割点.
点评 本题考查的是黄金分割的定义,把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,它们的比值($\frac{\sqrt{5}-1}{2}$)叫做黄金比.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
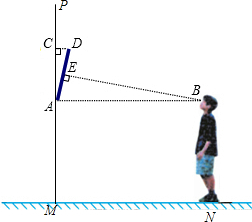 我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳,如图是小然站咋地面MN欣赏悬挂在墙壁PM上的油画AD(PM⊥MN)的示意图,设油画AD与墙壁的夹角∠PAD=α,此时小然的眼睛与油画底部A处于同一水平线上,视线恰好落在油画的中心位置E处,且与AD垂直.已知油画的高度AD为100cm.
我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳,如图是小然站咋地面MN欣赏悬挂在墙壁PM上的油画AD(PM⊥MN)的示意图,设油画AD与墙壁的夹角∠PAD=α,此时小然的眼睛与油画底部A处于同一水平线上,视线恰好落在油画的中心位置E处,且与AD垂直.已知油画的高度AD为100cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
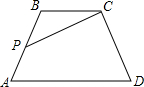 如图,已知AD∥BC,点P位AB上一点,设∠BCP=∠a,∠CPB=∠β.
如图,已知AD∥BC,点P位AB上一点,设∠BCP=∠a,∠CPB=∠β.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
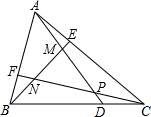 如图,在面积为1的△ABC中,点D,E,F分别在边BC,CA,AB上,且$\frac{BD}{DC}$=$\frac{CE}{EA}$=$\frac{AF}{FB}$=k>1,连接AD,BE,CF,得△PMN,则△PMN的面积为$\frac{{k}^{2}-2k+1}{{k}^{2}+k+1}$.
如图,在面积为1的△ABC中,点D,E,F分别在边BC,CA,AB上,且$\frac{BD}{DC}$=$\frac{CE}{EA}$=$\frac{AF}{FB}$=k>1,连接AD,BE,CF,得△PMN,则△PMN的面积为$\frac{{k}^{2}-2k+1}{{k}^{2}+k+1}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
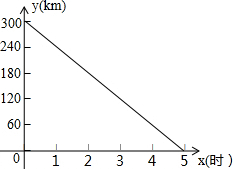 某货运公司甲乙两辆汽车,分别从AB两地同时以相同的速度发车,驾车驶往B城,乙车驶往A城,甲车与B城的距离y甲(km)与行驶时间x(时)的关系如图.
某货运公司甲乙两辆汽车,分别从AB两地同时以相同的速度发车,驾车驶往B城,乙车驶往A城,甲车与B城的距离y甲(km)与行驶时间x(时)的关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2ab)3=6a3b3 | B. | $\frac{-a-b}{a-b}$=-1 | C. | (-2)-2=-$\frac{1}{4}$ | D. | $\sqrt{(-3)^{2}}$=3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com