练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．某林场2011年造林200公顷，到2013年止，计划三年共造林728公顷，求每年造林面积的平均增长率是多少？

    分析 设每年造林面积的平均增长率为x，依照题意可得200+200（1+x）+200（1+x）2=728，解方程可知每年造林面积的年平均增长率．

    解答 解：设每年造林面积的平均增长率为x，
    依照题意可得
    200+200（1+x）+200（1+x）2=728，
    200（1+x）2+200（1+x）-528=0，
    （1+x）2+（1+x）-2.64=0，
    [（1+x）-1.2][（1+x）+2.2]=0，
    1+x=1.2，x=0.2=20%，
    1+x=-2.2，x=-3.2（不合题意，舍去）．
    答：每年造林面积的平均增长率为20%．

    点评 本题考查了一元二次方程的应用，根据题意分别表示出2012年和2013年造林的面积是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    16．6月5日（世界环境日），某市发布了一份空气质量抽样调查报告．该市1-5月随机调查的30天的空气质量级别列表统计如下：
     空气污染指数 0～50 51～100 101～150 151～200 201～250 300以上
     空气质量级别 优 良 轻微污染 轻度污染 中度污染 严重污染
     天　数6 12 542 1
    你估计该市一年空气质量的主要级别是良．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图，若∠1=∠2，则下列结论正确的是（　　）
    A．AB∥CDB．AD∥BCC．∠ABD=∠BDCD．∠A=∠C

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

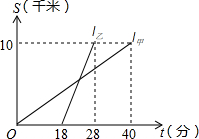    14．甲、乙两人以相同路线前往距离单位10km的培训中心参加学习．图中l甲，l乙分别表示甲、乙两人前往目的地所走的路程s（千米）随时间t（分）变化的函数图象．请你写出一个正确的说法：如答案不唯一，如①乙比甲提前12分钟到达；②甲的平均速度为15千米/小时；③乙走了10分钟就到达培训中心；等．．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

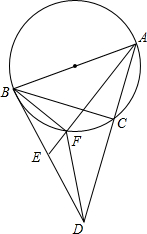    1．如图，已知在△ABC中，AB＞BC，过点B作△ABC的外接圆的切线，交AC的延长线于点D，E为BD的中点，连接AE交△ABC的外接圆于点F，求证：∠CBF=∠BDF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知线段AB=a，在线段AB上有一点C，若AC=$\frac{3-\sqrt{5}}{2}$a，则点C是线段AB的黄金分割点吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

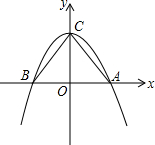    18．如图，抛物线y=-$\frac{1}{2}$x2+2与x轴交于A、B两点，其中点A在x轴的正半轴上，点B在x轴的负半轴上
    （1）试写出该抛物线的对称轴和顶点C的坐标；
    （2）问在抛物线上是否存在一点M，使△MAC≌△OAC？若存在，求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．（1）操作发现：如图①，D是等边△ABC边BA上一动点（点D与点B不重合），连接DC，以DC为边在BC上方作等边△DCF，连接AF．直接写出线段AF与BD之间的数量关系．
    （2）类比猜想：如图②，当△ABC为以BC为斜边的等腰直角三角形，D是△ABC边BA上一动点（点D 与点B不重合），连接DC，以DC为斜边在BC上方作等腰直角△FDC，连接AF． 请直接写出它们的数量关系．
    （3）深入探究：
    Ⅰ．如图③，当△ABC为以BC为底边的等腰三角形，D是△ABC边BA上一动点（点D与点B不重合），连接DC，以DC为底边在BC上方作等腰△FDC，∠BC A=∠DCF，且∠BAC=α，连接AF．线段AF与BD之间的有什么数量关系？证明你发现的结论；
    Ⅱ．如图④，当△ABC为任意三角形，D是△ABC边BA上一动点（点D与点B不重合），连接DC，以DC为边在BC上方作△FDC∽△ABC，且$\frac{BC}{AC}$=k，连接AF．线段AF与BD之间的有什么数量关系？直接写出你发现的结论．

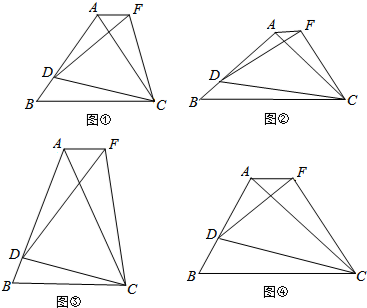
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

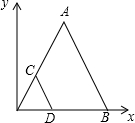    16．如图，把△COD扩大后得到△AOB，若点C，D，B的坐标分别为C（1，2），D（2，0），B（5，0）．则点A的坐标为（　　）
    A．（2，5）B．（2.5，5）C．（2，5）D．（3，6）

    查看答案和解析>>

    同步练习册答案