
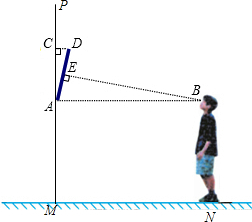
 我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳,如图是小然站咋地面MN欣赏悬挂在墙壁PM上的油画AD(PM⊥MN)的示意图,设油画AD与墙壁的夹角∠PAD=α,此时小然的眼睛与油画底部A处于同一水平线上,视线恰好落在油画的中心位置E处,且与AD垂直.已知油画的高度AD为100cm.
我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳,如图是小然站咋地面MN欣赏悬挂在墙壁PM上的油画AD(PM⊥MN)的示意图,设油画AD与墙壁的夹角∠PAD=α,此时小然的眼睛与油画底部A处于同一水平线上,视线恰好落在油画的中心位置E处,且与AD垂直.已知油画的高度AD为100cm.分析 (1)利用线段垂直平分线的性质得出AB=BD,则∠ABE=∠DBE,进而得出答案;
(2)可根据sin∠CAD=$\frac{CD}{AD}$直接求出CD的值;利用△ACD∽△BEA,根据相似三角形的对应边成比例解答;
(3)利用(1)可知视角变小,则需要远离墙壁.进而得出答案.
解答 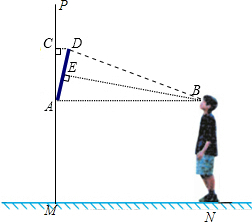 解:(1)连接BD,
解:(1)连接BD,
∵∠CAD+∠BAD=90°,∠BAD+∠ABE=90°,
∴∠CAD=∠ABE,
∵AE=DE,BE⊥AD,
∴∠ABE=∠DBE,
∴∠ABD=2α;
(2)如图,过点D作DC⊥PM交PM于点C,
解法一:
在Rt△ACD中,
∵sin∠CAD=$\frac{CD}{AD}$=sinα=$\frac{AE}{AB}$=$\frac{50}{250}$=$\frac{1}{5}$,
∴CD=$\frac{1}{5}$AD=$\frac{1}{5}$×100=20(cm),
解法二:
∵∠CAD=∠ABE=α,
∠ACD=∠AEB=90°,
∴△ACD∽△BEA,
∴$\frac{CD}{AE}$=$\frac{AD}{AB}$,
∴$\frac{CD}{50}$=$\frac{100}{250}$,
∴CD=20(cm),
∴镜框顶部到墙壁的距离CD是20cm;
(3)当油画底部A处位置不变,油画AD与墙壁的夹角逐渐减小时,小然为了保证欣赏油画的视觉效果最佳,
他应该远离墙壁PM.
点评 此题主要考查了相似三角形的应用以及视角问题,根据线段垂直平分线的性质得出AB=BD是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
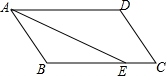 如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )| A. | 4和1 | B. | 1和4 | C. | 3和2 | D. | 2和3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
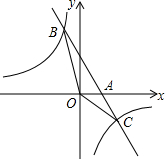 如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5)、C($\frac{5}{2}$,d)两点.
如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5)、C($\frac{5}{2}$,d)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 空气污染指数 | 0~50 | 51~100 | 101~150 | 151~200 | 201~250 | 300以上 |
| 空气质量级别 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 严重污染 |
| 天 数 | 6 | 12 | 5 | 4 | 2 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知线段AB=a,在线段AB上有一点C,若AC=$\frac{3-\sqrt{5}}{2}$a,则点C是线段AB的黄金分割点吗?为什么?
已知线段AB=a,在线段AB上有一点C,若AC=$\frac{3-\sqrt{5}}{2}$a,则点C是线段AB的黄金分割点吗?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com