
 将两个斜边长相等的三角形纸片如图放置,其中∠ACB=∠CED=90°,∠A=45°,∠CDE=30°,∠BCE=15°,则∠ABD的度数为( )
将两个斜边长相等的三角形纸片如图放置,其中∠ACB=∠CED=90°,∠A=45°,∠CDE=30°,∠BCE=15°,则∠ABD的度数为( )| A、40° | B、45° |
| C、50° | D、60° |
| 1 |
| 2 |
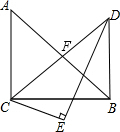 解:如图,设AB、CD相交于点F,
解:如图,设AB、CD相交于点F,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| A、30πcm2 |
| B、15πcm2 |
| C、12πcm2 |
| D、20πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
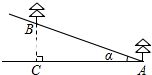 如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.5米范围内,问小明种植的这两棵树是否符合这个要求?
如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.5米范围内,问小明种植的这两棵树是否符合这个要求?查看答案和解析>>
科目:初中数学 来源: 题型:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 |
| A、(-1,0) |
| B、(0,-3) |
| C、(1,-4) |
| D、(2,-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com