练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    某航空公司规定，乘客所携带行李的重量x（kg）与运费y（元）满足如图所示的函数图象，那么每位乘客最多可免费携带
     
    kg的行李．
    考点：一次函数的应用
    专题：
    分析：设乘客所携带行李的重量x（kg）与运费y（元）之间的函数关系式为y=kx+b，由待定系数法求出其解即可．
    解答：解：设乘客所携带行李的重量x（kg）与运费y（元）之间的函数关系式为y=kx+b，由题意，得
    300=30k+b
    900=50k+b
    ，
    解得：
    k=30
    b=-600
    ，
    则y=30x-600．
    当y=0时，
    30x-600=0，
    解得：x=20．
    故答案为：20．
    点评：本题考查了运用待定系数法求一次函数的解析式的运用，由函数值求自变量的值的运用，解答时求出函数的解析式是关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系xOy中，已知A、B两点分别在x轴、y轴上．以AB为一边，作等腰△ABC，若点C在y轴上，则符合题意的C点有
     
    个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    将两个斜边长相等的三角形纸片如图放置，其中∠ACB=∠CED=90°，∠A=45°，∠CDE=30°，∠BCE=15°，则∠ABD的度数为（　　）
    A、40°B、45°
    C、50°D、60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    钟表上的时间是2时30分，此时时针与分针所成的夹角是
     
    度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知反比例函数
    a-3
    x
    的图象位于一、三象限，则a的取值范围是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

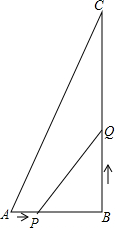    如图所示，在△ABC中，∠B=90°，△ABC三边长为整数且两直角边的长为关于x的一元二次方程x2-7x+（2k+8）=0的两实数根，其中k为正整数，且AB＜BC．
    （1）求△ABC的三边长；
    （2）点P从A点开始沿AB边向点B以1个单位长/秒的速度移动，而点Q从B点开始沿BC边向C以2个单位长/秒的速度移动，如果P，Q分别从A，B同时出发，经过几秒钟，△PBQ的面积为△ABC面积的
    1
    3
    ？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    命题：①等弧所对的圆周角相等；②三角形的外心到三角形各顶点的距离都相等；③三点确定一个圆；④圆的切线垂直于半径．其中不正确的有（　　）
    A、1个B、2个C、3个D、4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    点P（a-1，5）和点Q（2，b-2）关于x轴对称，则（a+b）2007的值为（　　）
    A、0
    B、-1
    C、1
    D、（-3）2007

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知二次函数y=-x2-2x+k的图象经过点A（2，y1），B（-2，y2），C（-5，y3），则下列结论正确的是（　　）
    A、y1＜y2＜y3
    B、y2＜y1＜y3
    C、y3＜y1＜y2
    D、y1＜y3＜y2

    查看答案和解析>>

    同步练习册答案