
【题目】如图,在△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B的路径运动,且速度为每秒2cm,设点P的运动时间为t秒.
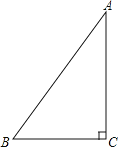
(1)则AC=______cm;
(2)当BP平分∠ABC,求此时点P的运动时间t的值;
(3)点P运动过程中,△BCP能否成为等腰三角形?若能,求出t的值;若不能请说明理由.
【答案】(1)4;(2)![]() ;(3)t为
;(3)t为![]() s或
s或![]() s或3s或
s或3s或![]() s时,△BCP为等腰三角形.
s时,△BCP为等腰三角形.
【解析】
(1)直接由勾股定理得,可得AC的值;
(2)作PE⊥AB于E,可得△BPE≌△BPC,可得BE=BC=3,PE=PC,AE=5-BE=2,AP=4-PC,在Rt△AEP中,AP2=AE2+EP2,即(4-PC)2=22+PC2,可得PC的值,可得时间.
(3)分CP=CB,BP=BC=3,CP=CB=3,PC=PB 几种情况讨论可得t的值.
解:(1)由勾股定理得,AC=![]() =4(cm),
=4(cm),
故答案为:4;
(2)作PE⊥AB于E,

在△BPE和△BPC中,
 ,
,
∴△BPE≌△BPC(AAS)
∴BE=BC=3,PE=PC,
∴AE=5-BE=2,AP=4-PC,
在Rt△AEP中,AP2=AE2+EP2,即(4-PC)2=22+PC2,
解得,PC=![]() ,
,
当BP平分∠ABC时,点P的运动时间t=![]() ÷2=
÷2=![]() 秒;
秒;
(3)如图2,当CP=CB时,△BCP为等腰三角形,

若点P在CA上,则2t=3,
解得t=![]() (s);
(s);
如图3,当BP=BC=3时,△BCP为等腰三角形,

∴AP=AB-BP=2,
∴t=(4+2)÷2=3(s);
如图4,若点P在AB上,CP=CB=3,作CD⊥AB于D,则根据面积法求得CD=![]() ,
,

在Rt△BCD中,由勾股定理得,BD=![]() ,
,
∴PB=2BD=![]()
∴CA+AP=4+5-![]() =5.4,
=5.4,
此时t=5.4÷2=2.7(s);
如图5,当PC=PB时,△BCP为等腰三角形,作PD⊥BC于D,则BD=CD,

∴PD为△ABC的中位线,
∴AP=BP=![]() AB=
AB=![]() ,
,
∴t=(4+![]() )÷2=
)÷2=![]() (s);
(s);
综上所述,t为![]() s或
s或![]() s或3s或
s或3s或![]() s时,△BCP为等腰三角形;
s时,△BCP为等腰三角形;


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有黑球两个,白球三个,这些小球除颜色外无其他区别,从袋子中随机摸出一个小球后,放回并摇匀,再随机摸出一个小球,则两次摸出的小球都是黑球的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
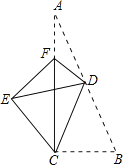
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=2![]() ,BC=2,点D为斜边AB的中点,连接CD,将△BCD沿CD翻折,使点B落在点E处,点F为直角边AC上一点,连接DF,将△ADF沿DF翻折,使点A与点E重合,求折痕DF的长.
,BC=2,点D为斜边AB的中点,连接CD,将△BCD沿CD翻折,使点B落在点E处,点F为直角边AC上一点,连接DF,将△ADF沿DF翻折,使点A与点E重合,求折痕DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某街道改建工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书. 从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天可以完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天可以完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为0.84万元,乙队每天的施工费用为0.56万元,工程预算的施工费用为50万元. 为缩短工期以减少对住户的影响,拟安排甲、乙两队合作完成这项工程,则工程预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠ACB=90°,∠A=α,以C为中心将△ABC旋转θ角到△A1B1C(旋转过程中保持△ABC的形状大小不变)B点恰落在A1B1上,如图,则旋转角θ的大小为( ) 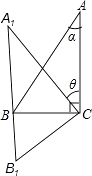
A.α+10°
B.α+20°
C.α
D.2α
查看答案和解析>>
科目:初中数学 来源: 题型:
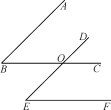
【题目】如图,已知BC,DE相交于点O,给出以下三个判断:①AB∥DE;②BC∥EF;③∠B=∠E,请你以其中两个判断作为题设,另外一个判断作为结论,写出所有的命题,指出这些命题是真命题还是假命题,并选择其中的一个真命题加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图1所示,通道由在同一平面内的AB,BC,CA,OA,OB,OC组成.为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器.设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为( )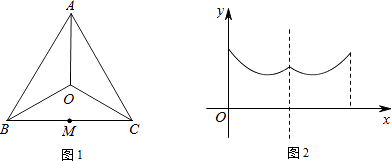
A.A→O→B
B.B→A→C
C.B→O→C
D.C→B→O
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com