
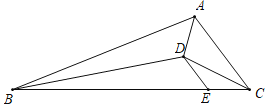
【题目】在△ABC中,AC=6,AB=14,BC=16,点D是△ABC的内心,过D作DE∥AC交BC于E,则DE的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
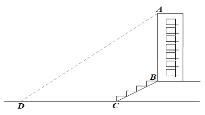
【题目】某班的同学想测量一教楼AB的高度.如图,大楼前有一段斜坡![]() ,已知
,已知![]() 的长为16米,它的坡度
的长为16米,它的坡度![]() .在离
.在离![]() 点45米的
点45米的![]() 处,测得一教楼顶端
处,测得一教楼顶端![]() 的仰角为
的仰角为![]() ,则一教楼
,则一教楼![]() 的高度约( )米(结果精确到0.1米)(参考数据:
的高度约( )米(结果精确到0.1米)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
A. 44.1 B. 39.8 C. 36.1 D. 25.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的ALMN,若中间空白部分四边形OPQR恰好是正方形,且ALMN的面积为50,则正方形EFGH的面积为( )
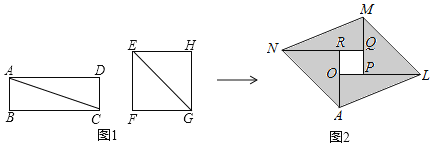
A. 24 B. 25 C. 26 D. 27
查看答案和解析>>
科目:初中数学 来源: 题型:
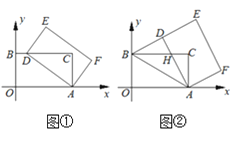
【题目】在平面直角坐标系中,点![]() 是原点,四边形
是原点,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() .以点
.以点![]() 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() .
.
(1)如图①,当点![]() 落在
落在![]() 边上时,求点
边上时,求点![]() 的坐标;
的坐标;
(2)如图②,当点![]() 落在线段
落在线段![]() 上时,
上时,![]() 与
与![]() 交于点
交于点![]() .求点
.求点![]() 的坐标;
的坐标;
(3)记![]() 为矩形
为矩形![]() 对角线的交点,
对角线的交点,![]() 为
为![]() 的面积,求
的面积,求![]() 的取值范围(直接写出结果即可).
的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
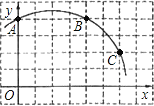
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)在图中确定该圆弧所在圆的圆心D点的位置,并写出点D点坐标为________.
(2)连接AD、CD,求⊙D的半径及![]() 的长;
的长;
(3)有一点E(6,0),判断点E与⊙D的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
(1)求顶点D的坐标(用含m的代数式表示);
(2)当抛物线过点(1,-2),且不经过第一象限时,平移此抛物线到抛物线![]() 的位置,求平移的方向和距离;
的位置,求平移的方向和距离;
(3)当抛物线顶点D在第二象限时,如果∠ADH=∠AHO,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=3,点E是边CD的中点,点P,Q分别是射线DC与射线EB上的动点,连结PQ,AP,BP,设DP=t,EQ=![]() t.
t.
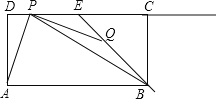
(1)当点P在线段DE上(不包括端点)时.
①求证:AP=PQ;②当AP平分∠DPB时,求△PBQ的面积.
(2)在点P,Q的运动过程中,是否存在这样的t,使得△PBQ为等腰三角形?若存在,请求出t的值;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于G,连接AG,现在有如下四个结论:①∠EAG=45°;②FG=FC;③FC∥AG;④S△GFC=14.其中结论正确的序号是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com