
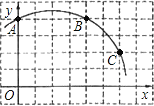
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)在图中确定该圆弧所在圆的圆心D点的位置,并写出点D点坐标为________.
(2)连接AD、CD,求⊙D的半径及![]() 的长;
的长;
(3)有一点E(6,0),判断点E与⊙D的位置关系.
科目:初中数学 来源: 题型:
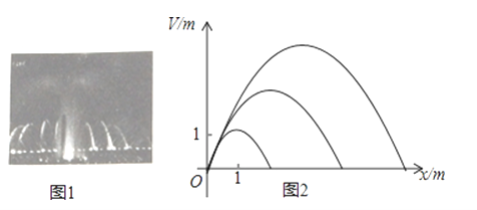
【题目】音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a、b的值;
(2)若k=1,喷出的水恰好达到岸边,则此时喷出的抛物线水线最大高度是多少米?
(3)若k=3,a=﹣![]() ,则喷出的抛物线水线能否达到岸边?
,则喷出的抛物线水线能否达到岸边?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国高铁迅猛发展,给我们的出行带来极大的便捷,如图1,是某种新设计动车车头的纵截面一部分,曲线OBA是一开口向左,对称轴正好是水平线OC的抛物线的一部分,点A、B是车头玻璃罩的最高点和最低点,AC、BD是两点到车厢底部的距离,OD=1.5米,BD=1.5米,AC=3米,请你利用所学的函数知识解决以下问题.
(1)为了方便研究问题,需要把曲线OBA绕点O旋转转化为我们熟悉的函数,请你在所给的方框内,画出你旋转后函数图象的草图,在图中标出点O、A、B、C、D对应的位置,并求你所画的函数的解析式.
(2)如图2,驾驶员座椅安装在水平线OC上一点P处,实验表明:当PA+PB最小时,驾驶员驾驶时视野最佳,为了达到最佳视野,求OP的长.
(3)驾驶员头顶到玻璃罩的高度至少为0.3米才感到压抑,一个驾驶员坐下时头顶到椅面的距离为1米,在(2)的情况下,座椅最多条件到多少时他才感到舒适?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标
(3)已知点D(m,m+1)在第一象限的抛物线上,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
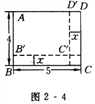
【题目】如图2 - 4所示,长方形ABCD的长为5 cm,宽为4 cm,如果将它的长和宽都减去x(cm),那么它剩下的小长方形AB′C′D′的面积为y(cm2).
(1)写出y与x的函数关系式;
(2)上述函数是什么函数?
(3)自变量x的取值范围是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
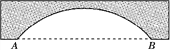
【题目】如图,一拱形公路桥,圆弧形桥拱的水面跨度AB=80 m,桥拱到水面的最大高度为20 m.(1)求桥拱的半径.
(2)现有一艘宽60 m,顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,AB=BC,∠B=∠C=90°,P是BC边上一点,AP⊥PD,E是AB边上一点,∠BPE=∠BAP.
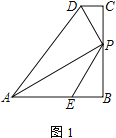
(1) 如图1,若AE=PE,直接写出![]() =______;
=______;
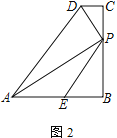
(2) 如图2,求证:AP=PD+PE;
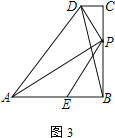
(3) 如图3,当AE=BP时,连BD,则![]() =______,并说明理由.
=______,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)(x-1)2﹣9=0;
(2)3(x+5)=(x+5)2;
(3)x2+6x-55=0;
(4)2x(x+3)-1=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com