
如图所示,AB为半圆O的直径,点D是半圆弧的中点,半径OC∥BD,过点C作AD的平行线交BA延长线于点E.
(1)判断CE与半圆OD的位置关系,并证明你的结论.
(2)若BD=4,求阴影部分面积.


【考点】切线的判定;扇形面积的计算.
【分析】(1)直接利用圆周角定理结合平行线的性质得出CO⊥EC,即可得出答案;
(2)利用已知得出△ADB为等腰直角三角形,进而得出△ECO为等腰直角三角形,由S阴影部分=S△ECD﹣S扇形AOC求出答案.
【解答】解:(1)CE与半圆OD相切,
理由:∵AB为直径,
∴∠ADB=90°,
∴AD⊥DB,
∵CO∥DB,
∴CO⊥AD,
∵EC∥AD,
∴CO⊥EC,
∴CE与半圆OD相切;
(2)∵点D平分半圆弧,
∴∠B=45°,
∴△ADB为等腰直角三角形,
∵BD=4,
∴AB=4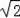
 ,
,
∴CO=2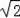
 ,
,
∵CO∥DB,
∴∠AOC=∠ABD=45°,
由(1)知CO⊥EC,
∴△ECO为等腰直角三角形,
∴S阴影部分=S△ECD﹣S扇形AOC=
 (2
(2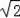
 )2﹣
)2﹣
 π(2
π(2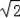
 )2=4﹣π.
)2=4﹣π.
【点评】此题主要考查了切线的判定以及等腰直角三角形的性质、扇形面积求法等知识,正确得出△ECO为等腰直角三角形是解题关键.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
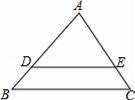
如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )

A.6 B.4.5 C.2 D.1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
问题背景:△AOB、△COD是两个等腰直角三角形,现将直角顶点以及两直角边都重合在一起,如图1所示,点P是CD中点,连接BP并延长到E使PE=BP,连接EC,作平行四边形ACEF,小林针对平行四边形ACEF形状进行了如下探究:
观察操作:(1)小林先假设小等腰直角三角形的直角边非常小,这时三角形可以看作一个点,如图2所示,并提出猜想四边形ACEF是 ;
猜想证明:(2)小林对比图1和图2的情形,完成了(1)中的猜想,请借助图1帮他证明这个猜想.
拓展延伸:(3)如图3所示,现将等腰直角三角形COD绕点O逆时针旋转一定角度,其它条件都不改变,原来结论是否仍然成立?请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
小明手里有6张完全一样的卡片,其中4张正面画上记号“A”,另外2张卡片被画上记号“B”,先将其背面朝上洗匀,让小东从中随机抽取2张卡片,则他抽出的两张均有“A”记号的卡片的概率等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )


A.圆 B.椭圆
C.一般的平行四边形 D.矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题中正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相垂直平分且相等的四边形是正方形
D.一组对边相等,另一组对边平行的四边形是平行四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com