
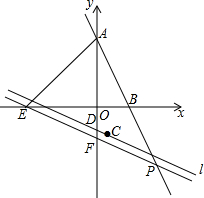
 如图,已知直线y=-2x+8和x轴、y轴分别交于B和A,直线l经过点C(2,-4)和D(0,-3),向下平移1个单位后与x轴、y轴分别交于点E,F,直线AB和EF相交于P.
如图,已知直线y=-2x+8和x轴、y轴分别交于B和A,直线l经过点C(2,-4)和D(0,-3),向下平移1个单位后与x轴、y轴分别交于点E,F,直线AB和EF相交于P.分析 (1)设直线l的解析式为y=kx+b,将C、D坐标代入,求出k、b的值,继而可求得解析式;
(2)①先求出直线向下平移1个单位后的解析式,得出点E、F的坐标,根据AB解析式求出A、B坐标,可得AO=EO,BO=FO,根据SAS证明△AOB≌△EOF;
②由①知△AOB≌△EOF,可得∠OAB=∠OEF,又根据OA=OE,得出∠OAE=∠OEA,可得∠PAE=∠PEA,最后判断△APE是等腰三角形.
解答 解:(1)设y=kx+b,
将C、D坐标代入得:$\left\{\begin{array}{l}{2k+b=-4}\\{b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-3}\end{array}\right.$,
即y=-$\frac{1}{2}$x-3;
(2)①直线向下平移1个单位后解析式为y=-$\frac{1}{2}$x-4,
∴E(-8,0),F(0,-4),
又∵直线y=-2x+8和x轴、y轴分别交于B和A,
∴A(0,8),B(4,0),
∴OE=OA=8,OF=OB=4,
在△AOB和△EOF中,
∵$\left\{\begin{array}{l}{OE=OA}\\{∠EOF=∠AOB}\\{OF=OB}\end{array}\right.$,
∴△AOB≌△EOF(SAS);
②△APE是等腰三角形.
由①知△AOB≌△EOF,
∴∠OAB=∠OEF,
又OA=OE,
∴∠OAE=∠OEA,
∴∠OAB+∠OAE=∠OEF+∠OEA,
即∠PAE=∠PEA,
∴△APE是等腰三角形.
点评 本题考查了一次函数的综合应用,涉及了待定系数法求解函数解析式、平移的性质、全等三角形的判定和性质以及等腰三角形的判定,知识点较多,难度适中.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | x2-2=(x-1)(x+1)-1 | B. | (a+b)(a-b)=a2-b2 | C. | 1-x2=(1+x)(1-x) | D. | x2+4=(x+2)2-4x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
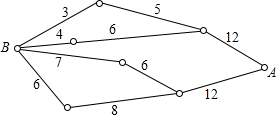 如图所示,小圆圈表示网络的结点,结点之间的线段表示它们有网线相连.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息分开可以从不同的路线同时传递,则单位的时间内传递的最大信息量为( )
如图所示,小圆圈表示网络的结点,结点之间的线段表示它们有网线相连.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息分开可以从不同的路线同时传递,则单位的时间内传递的最大信息量为( )| A. | 19 | B. | 20 | C. | 24 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
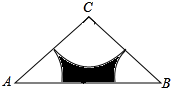 如图,在△ABC中,∠C=120°,CA=CB=6,分别以A,B,C为圆心,以3为半径画弧,三条弧与AB所围成的阴影部分的周长是3π+6$\sqrt{3}$-6.
如图,在△ABC中,∠C=120°,CA=CB=6,分别以A,B,C为圆心,以3为半径画弧,三条弧与AB所围成的阴影部分的周长是3π+6$\sqrt{3}$-6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com