练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
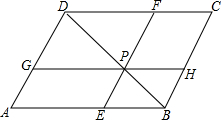
    19．如图，在?ABCD中，P是对角线BD上的一点，过P点的直线EF∥BC．GH∥AB．则图中面积相等的四边形有5对．

    分析 根据平行四边形的对角线把平行四边形分成两个面积相等的三角形，再根据等式的性质即可解决问题．

    解答 解：∵四边形ABCD是平行四边形
    ∴S△ABD=S△CBD．
    ∵BP是平行四边形BEPH的对角线，
    ∴S△BEP=S△BHP，
    ∵PD是平行四边形GPFD的对角线，
    ∴S△GPD=S△FPD．
    ∴S△ABD-S△BEP-S△GPD=S△BCD-S△BHP-S△PFD，即S?AEPG=S?HCFP，
    ∴S?AEPG+S四边形PEHB，=S?HCFP+S四边形PEBH，
    ∴S?ABHG=S?BCFE，
    同理S?AEFD=S?HCDG．
    即：S?ABHG=S?BCFE，S?AGPE=S?HCFP，S?AEFD=S?HCDG，S梯形ABPG=S梯形CDPH，S梯形AEPD=S梯形CHPD．故答案为5．

    点评 本题考查的是平行四变形的性质，平行四边形的一条对角线可以把平行四边形分成两个全等的三角形，两条对角线把平行四边形的面积一分为四，解题的关键是等式性质的灵活运用，属于中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    9．4的算术平方根是2，5的平方根是±$\sqrt{5}$，-27的立方根是-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．在平行四边形ABCD中，如果∠A=68°，那么∠B=112°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

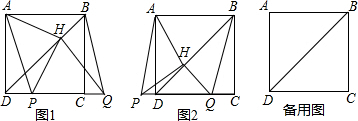
    7．在平行四边形ABCD中，过点D作DE⊥AB于点E，点F在边CD上，DF=BE，连接AF，BF．
    （1）求证：四边形BFDE为矩形；
    （2）若AE=3，BF=4，AF平分∠DAB，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，在?ABCD中，E，F为对角线AC上的两点，且AE=CF，连接DE，BF，求证：DE∥BF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．在正方形ABCD中，BD是一条对角线，点P在直线CD上（不与点C、D重合），连接AP，平移△ADP，使点D移动到点C，得到△BCQ，过点Q作QH⊥BD于H，连接AH，PH．
    （1）问题发现：如图1，若点P在线段CD上，AH与PH的数量关系是AH=PH，位置关系是AH⊥PH；
    （2）拓展探究：如图2，若点P在线段CD的延长线上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给出证明，否则说明理由；
    （3）解决问题：若点P在线段DC的延长线上，且∠AHQ=120°，正方形ABCD的边长为2，请直接写出求DP的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，在?ABCD中，BE平分∠ABC交AD于点E，CF平分∠BCD交AD于点F，AB=3，AD=5，则EF的长为1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

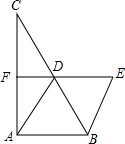    8．如图，△ABC中，AD是BC边的中线，分别过点B，D作AD，AB的平行线交于点E，且ED交AC于点F，AD=2DF．
    （1）求证：四边形ABED为菱形；
    （2）若BD=6，∠E=60°，求四边形ABED的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，已知锐角∠MBN的正切值等于3，△PBD中，∠BDP=90°，点D在∠MBN的边BN上，点P在∠MBN内，PD=3，BD=9，直线l经过点P，并绕点P旋转，交射线BM于点A，交射线DN于点C，设$\frac{CA}{CP}$=x
    （1）求x=2时，点A到BN的距离；
    （2）设△ABC的面积为y，求y关于x的函数解析式，并写出函数的定义域；
    （3）当△ABC因l的旋转成为等腰三角形时，求x的值．

    查看答案和解析>>

    同步练习册答案