
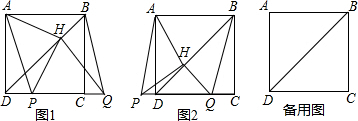
分析 (1)连接HC,根据正方形的性质、等腰直角三角形的性质得到△HDP≌△HQC,根据全等三角形的性质得到HP=HC,∠DHP=∠QHC,根据正方形是轴对称图形证明结论;
(2)同(1)的证明方法相同,根据图形证明即可;
(3)由(1)的结论AH=PH,AH⊥PH,得出∠HPA=45°,推导出∠APD=30°,再由三角函数即可求解.
解答 解:(1)AH=PH,AH⊥PH,
理由如下:如图1,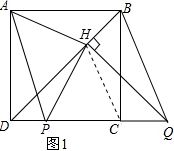 连接HC,
连接HC,
∵四边形ABCD是正方形,
∴∠BDC=45°,又QH⊥BD,
∴△DHQ是等腰直角三角形,
由平移的性质可知DP=CQ,
在△HDP和△HQC中,
$\left\{\begin{array}{l}{HD=HQ}\\{∠HDP=∠HQC}\\{DP=QC}\end{array}\right.$,
∴△HDP≌△HQC,
∴HP=HC,∠DHP=∠QHC,
根据正方形是轴对称图形得到HA=HC,∠AHD=∠CHD,
∴HA=HP,AH⊥PH;
故答案为:HA=HP,AH⊥PH;
(2)(1)中的结论仍然成立,
如图2,连接HC,
根据正方形是轴对称图形得到HA=HC,∠AHD=∠CHD,
AH=PH,AH⊥PH,
理由如下:如图2,连接HC,
∵四边形ABCD是正方形,
∴∠BDC=45°,又QH⊥BD,
∴△DHQ是等腰直角三角形,
∴∠HDP=∠HQC=135°,
由平移的性质可知DP=CQ,
在△HDP和△HQC中,
$\left\{\begin{array}{l}{HD=HQ}\\{∠HDP=∠HQC}\\{PD=CQ}\end{array}\right.$,
∴△HDP≌△HQC,
∴HP=HC,∠DHP=∠QHC,
∴HA=HP,AH⊥PH;
(3)由(1)知,AH=PH,AH⊥PH,
∴∠HPA=45°,
∵∠AHQ=120°,
∴∠AHB=∠CHB=30°,
∴∠QHP=∠CHB=∠CHP=30°,
∴∠CPH=75°,
∴∠APD=30°,
在Rt△ADP中,AD=2,
∴DP=2$\sqrt{3}$.
点评 本题考查的是四边形综合题,涉及到正方形的性质、图形平移的性质、全等三角形的判定与性质等知识,难度适中,解决本题的关键是熟记全等三角形的性质定理和判定定理.


科目:初中数学 来源: 题型:解答题
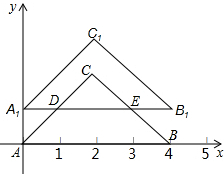 如图,等腰直角三角形ABC中,∠C=90°,A(0,0),B(4,0),点C在x轴上方,把△ABC向上平移1个单位后,得到△A1B1C1,且A1B1分别交AC于点D,交BC于点E.
如图,等腰直角三角形ABC中,∠C=90°,A(0,0),B(4,0),点C在x轴上方,把△ABC向上平移1个单位后,得到△A1B1C1,且A1B1分别交AC于点D,交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
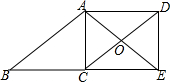 如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.
如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
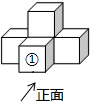 如图所示的几何体是由5个大小相同的小正方体摆成的,若取走小正方体①,下列说法正确的是( )
如图所示的几何体是由5个大小相同的小正方体摆成的,若取走小正方体①,下列说法正确的是( )| A. | 主视图与左视图不变 | B. | 左视图与俯视图不变 | ||
| C. | 主视图与俯视图改变 | D. | 左视图与俯视图改变 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com