
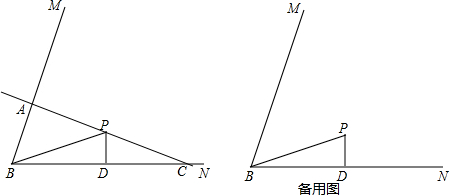
分析 (1)由PD∥AH得到$\frac{AH}{PD}=\frac{CA}{CP}$=2,即可;
(2)由PD∥AH得到$\frac{AH}{PD}=\frac{CA}{CP}$,再由tan∠MBN=3,比例式表示出BC,CD,即可;
(3)△ABC为等腰三角形时,分三种情况①AB=AC,②CB=CA,③BC=BA利用tan∠MBN=3,建立方程即可.
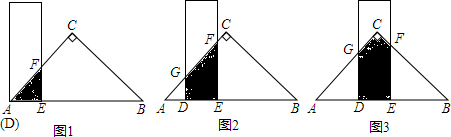
解答 解:(1)如图1,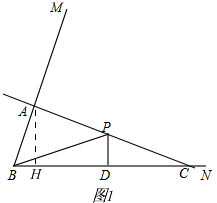
过点A作AH⊥BC,
∵PD⊥BC,
∴PD∥AH,
∴$\frac{AH}{PD}=\frac{CA}{CP}$=2,
∴AH=2PD=6,
(2)∵PD∥AH,
∴$\frac{CA}{CP}=\frac{AH}{PD}$=x,
∴AH=PD×x=3x,
∵tan∠MBN=3,
∴BH=3,
∵$\frac{CD}{HD}=\frac{PD}{AH}$,
∴$\frac{CD}{CD+9-x}=\frac{3}{3x}$,
∴CD=$\frac{9-x}{x-1}$,
∴BC=BD+CD=9+$\frac{9-x}{x-1}$=$\frac{8x}{x-1}$,
∴S△ABC=$\frac{1}{2}$AH×BC=$\frac{1}{2}$×3x×$\frac{8x}{x-1}$=$\frac{1{2x}^{2}}{x-1}$,
∴y=$\frac{1{2x}^{2}}{x-1}$(1<x≤9),
(3)①当AB=AC时,
∵tan∠PCB=tan∠MBC=3,
∴$\frac{PD}{CD}$=3,
∴CD=1,
∴BC=BD+CD=10,
∴$\frac{8x}{x-1}$=10,
∴x=5,
②当CB=CA时,如图2,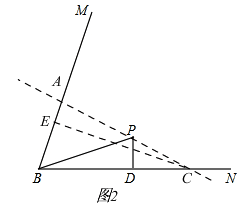
过点C作CE⊥AB,
BE=$\frac{1}{2}$AB=$\frac{\sqrt{10}}{2}$x,
∵tan∠MBN=3,
∴cos∠MBN=$\frac{\sqrt{10}}{10}$,
∴$\frac{BE}{BC}$=$\frac{\sqrt{10}}{10}$,
∴$\frac{\frac{\sqrt{10}}{2}x}{\frac{8x}{x-1}}=\frac{\sqrt{10}}{10}$,
∴x=$\frac{13}{5}$;
③当BA=BC时,$\sqrt{10}$x=$\frac{8x}{x-1}$,
∴x=1+$\frac{4\sqrt{10}}{5}$,
∴△ABC为等腰三角形时,x=5或$\frac{13}{5}$或1+$\frac{4\sqrt{10}}{5}$.
点评 此题是几何变换的综合题,主要考查平行线分线段成比例定理和锐角三角函数,由平行线分线段成比例定理建立方程是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 24x2y=3x•8xy | B. | m2-2m-3=m(m-2)-3 | C. | x2+2x+1=(x+1)2 | D. | (x+3)(x-3)=x2-9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
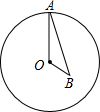 如图,点A为⊙O上一个动点,点B在⊙O内,且OA=2$\sqrt{3}$,OB=2,当∠OAB的度数取最大值时,AB的长度为2$\sqrt{2}$.
如图,点A为⊙O上一个动点,点B在⊙O内,且OA=2$\sqrt{3}$,OB=2,当∠OAB的度数取最大值时,AB的长度为2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
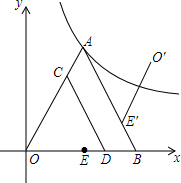 如图,在平面直角坐标系中,等边△OAB的顶点A落在反比例函数y=$\frac{9\sqrt{3}}{x}$上,OB在x轴正半轴上,中点为E,C为边OA上一点,过点C作CD∥AB交OB于D,以CD所在直线为对称轴将线段OE作轴对称变换得O′E′,设OC的长为x.
如图,在平面直角坐标系中,等边△OAB的顶点A落在反比例函数y=$\frac{9\sqrt{3}}{x}$上,OB在x轴正半轴上,中点为E,C为边OA上一点,过点C作CD∥AB交OB于D,以CD所在直线为对称轴将线段OE作轴对称变换得O′E′,设OC的长为x.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com