
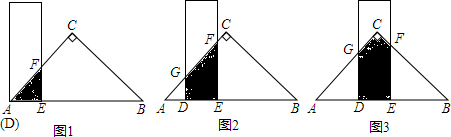
分析 (1)当x=0cm时,直尺和三角形纸板重叠部分的面积是两直角边都为4厘米的三角形面积;当x=4cm时,直尺和三角形纸板重叠部分的面积=两直角边都为8厘米的三角形面积-两直角边都为4厘米的三角形面积;当x=6cm时,直尺和三角形纸板重叠部分的面积=(两直角边都为8厘米的三角形面积-两直角边都为6厘米的三角形面积)×2,依此即可求解;
(2)根据阴影部分面积为26cm2,列出方程$\frac{1}{2}$(x+8)(8-x)+$\frac{1}{2}$(16-x-4+8)(4-8+x)=26,解方程即可求解.
解答 解:(1)当x=0cm时,S=4×4÷2=8cm2;
当x=4cm时,S=8×8÷2-4×4÷2=24cm2;
当x=6cm时,S=(8×8÷2-6×6÷2)×2=28cm2.
故答案为:8cm2;24cm2;28cm2.
(2)当S=26cm2时,x必然大于4,即$\frac{1}{2}$(x+8)(8-x)+$\frac{1}{2}$(16-x-4+8)(4-8+x)=26,
解得x1=6-$\sqrt{2}$,x2=6+$\sqrt{2}$.
故当x1=6-$\sqrt{2}$,x2=6+$\sqrt{2}$时,阴影部分面积为26cm2.
点评 本题考查了平移的性质,动点问题的函数图象,涉及的知识点有:直角三角形的面积,矩形的性质,梯形的面积,分类思想的应用,方程思想的应用,综合性较强,难度中等.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
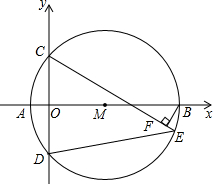 已知关于x的方程x2+(2m-6)x+m2-7=0有两个不相等的实数根,两根的平方和为10,且两根分别是A点和B点的横坐标(如图),以AB为直径作圆M交y轴于点C和点D,点E是$\widehat{BD}$上一点,BF⊥CE于点F,连接DE.
已知关于x的方程x2+(2m-6)x+m2-7=0有两个不相等的实数根,两根的平方和为10,且两根分别是A点和B点的横坐标(如图),以AB为直径作圆M交y轴于点C和点D,点E是$\widehat{BD}$上一点,BF⊥CE于点F,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
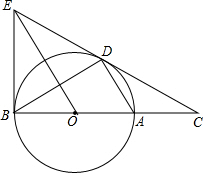 如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
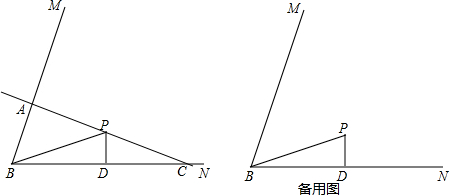
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
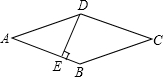 如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )
如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )| A. | 0.4 | B. | 0.5 | C. | 0.6 | D. | 0.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com