
【题目】如图,射线AM平行于射线BN,∠B=90°,AB=4,C是射线BN上的一个动点,连接AC,作CD⊥AC,且AC=2CD,过C作CE⊥BN交AD于点E,设BC长为a.
(1)求△ACD的面积(用含a的代数式表示);
(2)求点D到射线BN的距离(用含有a的代数式表示);
(3)是否存在点C,使△ACE是以AE为腰的等腰三角形?若存在,请求出此时a的值;若不存在,请说明理由.
【答案】
(1)
解:在Rt△ABC中,AB=4,BC=a,
∴AC= ![]() =
= ![]() ,
,
∴CD= ![]() AC=
AC= ![]() ,
,
∵∠ACD=90°,
∴S△ACD= ![]() ACCD=
ACCD= ![]()
(2)
解:如图1,过点D作DF⊥BN于点F,
∵∠FDC+∠FCD=90°,∠FCD+∠ACB=180°﹣90°=90°,
∴∠FDC=∠ACB,
∵∠B=∠DFC=90°,
∴∠FDC=∠ACB,
∵∠B=∠DFC=90°,
∴△DFC∽△CBA,
∴ ![]() ,
,
∴DF= ![]() BC=
BC= ![]() a,
a,
∴D到射线BN的距离为 ![]() a
a
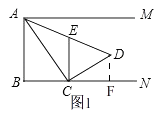
(3)
解:存在,①当EC=EA时,
∵∠ACD=90°,
∴EC=EA= ![]() AD,
AD,
∵AB∥CE∥DF,
∴BC=FC=a,
由(2)知,△DFC∽△CBA,
∴ ![]() ,
,
∴FC= ![]() AB=2,
AB=2,
∴a=2,
②当AE=AC时,如图2,AM⊥CE,
∴∠1=∠2,
∵AM∥BN,
∴∠2=∠4,
∴∠1=∠4,
由(2)知,∠3=∠4,
∴∠1=∠3,
∵∠AGD=∠DFC=90°,
∴△ADG∽△DCF,
∴ ![]() ,
,
∵AD= ![]() =
= ![]() ,AG=a+2,CD=
,AG=a+2,CD= ![]() ,
,
∴  ,
,
∴a=4 ![]() +8,
+8,
即:满足条件的a的值为2或4 ![]() +8.
+8.

【解析】(1)先根据勾股定理得出AC,进而得出CD,最后用三角形的面积公式即可;(2)先判断出∠FDC=∠ACB,进而判断出△DFC∽△CBA,得出 ![]() ,即可求出DF,即可;(3)分两种情况利用相似三角形的性质建立方程求解即可得出结论.
,即可求出DF,即可;(3)分两种情况利用相似三角形的性质建立方程求解即可得出结论.
【考点精析】本题主要考查了三角形的面积和勾股定理的概念的相关知识点,需要掌握三角形的面积=1/2×底×高;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,以线段AB为直径作⊙O,CD与⊙O相切于点E,交AB的延长线于点D,连接BE,过点O作OC∥BE交切线DE于点C,连接AC.
(1)求证:AC是⊙O的切线;
(2)若BD=OB=4,求弦AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.
A.7
B.11
C.13
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E. 
(1)求证:∠BDC=∠A;
(2)若CE=2 ![]() ,DE=2,求AD的长.
,DE=2,求AD的长.
(3)在(2)的条件下,求弧BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校运动会上,九(1)班啦啦队买了两种矿泉水,其中甲种矿泉水共花费80元,乙种矿泉水共花费60元.甲种矿泉水比乙种矿泉水多买20瓶,且乙种矿泉水的价格是甲种矿泉水价格的1.5倍.求甲、乙两种矿泉水的价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场进了一批家用空气净化器,成本为1200元/台.经调查发现,这种空气净化器每周的销售量y(台)与售价x(元/台)之间的关系如图所示: 
(1)请写出这种空气净化器每周的销售量y与 售价x的函数关系式(不写自变量的范围);
(2)若空气净化器每周的销售利润为W(元),则当售价为多少时,可获得最大利润,此时的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为km. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BA=AE=DC,AD=EC,CE⊥AE,垂足为E. 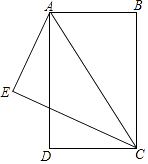
(1)求证:△DCA≌△EAC;
(2)只需添加一个条件,即 , 可使四边形ABCD为矩形.请加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+ax+b交x轴于A(1,0),B(3,0)两点,点P是抛物线上在第一象限内的一点,直线BP与y轴相交于点C. 
(1)求抛物线y=﹣x2+ax+b的解析式;
(2)当点P是线段BC的中点时,求点P的坐标;
(3)在(2)的条件下,求sin∠OCB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com