
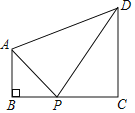
【题目】如图,四边形ABCD中,AB∥CD,∠B=90°,AB=1,CD=2,BC=m,点P是边BC上一动点,若△PAB与△PCD相似,且满足条件的点P恰有2个,则m的值为_______.
【答案】3或2![]() .
.
【解析】
由平行线得出∠C=90°,当∠BAP=∠CDP时,△PAB∽△PDC,得出![]() ,得出PC=2PB①,当∠BAP=∠CPD时,△PAB∽△DPC,得出
,得出PC=2PB①,当∠BAP=∠CPD时,△PAB∽△DPC,得出![]() ,即PB×PC=1×2=2②,由①②得:PB=1,得出PC=2,BC=3;
,即PB×PC=1×2=2②,由①②得:PB=1,得出PC=2,BC=3;
设BP=x,则=m-x,得出x:2=1:(m-x),整理得:x2-mx+2=0,方程有唯一解时,△=m2-8=0,解得:m=±2![]() (负值舍去),得出m=2
(负值舍去),得出m=2![]() ;即可得出结论.
;即可得出结论.
∵AB∥CD,∠B=90°,
∴∠C+∠B=180°,
∴∠C=90°,
当∠BAP=∠CDP时,△PAB∽△PDC,
∴![]() ,即
,即![]() ,
,
∴PC=2PB①,
当∠BAP=∠CPD时,△PAB∽△DPC,
∴![]() ,即PB×PC=1×2=2②,
,即PB×PC=1×2=2②,
由①②得:2PB2=2,
解得:PB=1,
∴PC=2,
∴BC=3;
设BP=x,则=m-x,
∴x:2=1:(m-x),
整理得:x2-mx+2=0,
方程有唯一解时,△=m2-8=0,
解得:m=±2![]() 负值舍去),
负值舍去),
∴m=2![]() ;
;
综上所述,若△PAB与△PCD相似,且满足条件的点P恰有2个,则m的值为3或2![]() ;
;
故答案为:3或2![]() .
.


科目:初中数学 来源: 题型:
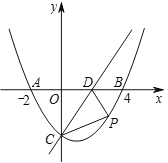
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求该抛物线的解析式.
(2)点![]() 是抛物线上第四象限上的一个动点,连接
是抛物线上第四象限上的一个动点,连接![]() ,
,![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
(3)将抛物线的对称轴向左平移3个长度单位得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若直线
,若直线![]() 上存在使
上存在使![]() 最大的点
最大的点![]() ,请直接写出满足条件的点
,请直接写出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
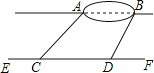
【题目】小明想测量湿地公园内某池塘两端A,B两点间的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=40°,再向前行走100米到点D处,测得∠BDF=52.44°,若直线AB与EF之间的距离为60米,求A,B两点的距离(结果精确到0.1)(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin52.44°≈0.79,cos52.44°≈0.61,tan52.44°≈1.30)
查看答案和解析>>
科目:初中数学 来源: 题型:
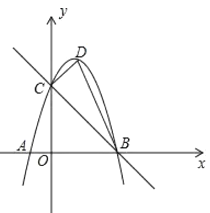
【题目】如图,以![]() 为顶点的抛物线
为顶点的抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 的表达式为
的表达式为![]() .
.
(1)求抛物线的表达式;
(2)求![]() 的面积;
的面积;
(3)在直线![]() 上有一点
上有一点![]() ,若使
,若使![]() 的值最小,则点
的值最小,则点![]() 的坐标为____________.
的坐标为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
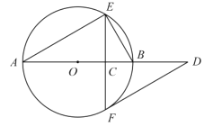
(1)已知![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,请补全图形;若
,请补全图形;若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
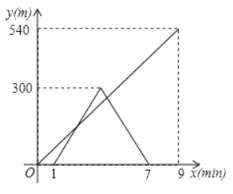
【题目】科技小组进行了机器人行走性实验,在实验场地有![]() 三点在同意笔直的赛道上,
三点在同意笔直的赛道上,![]() 两点之间的距离是540m,甲、乙两机器人分别从
两点之间的距离是540m,甲、乙两机器人分别从![]() 两点出发,甲机器人匀速按
两点出发,甲机器人匀速按![]() 的方向行走,乙机器人按
的方向行走,乙机器人按![]() 方向行走,乙先出发1min,甲再出发,甲、乙离各自出发点的距离
方向行走,乙先出发1min,甲再出发,甲、乙离各自出发点的距离![]() 与乙出发的时间
与乙出发的时间![]() 的函数关系式如图所示,结合图像回答下列问题:
的函数关系式如图所示,结合图像回答下列问题:
(1)甲的速度是__________m/min;乙的速度是________m/min;
(2)求甲机器人从C点返回A点时![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)乙机器人出发多长时间后两机器人相距80m.
查看答案和解析>>
科目:初中数学 来源: 题型:
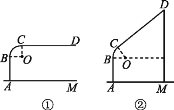
【题目】如图是一个桌面会议话筒示意图,中间BC部分是一段可弯曲的软管,在弯曲时可形成一段圆弧,设圆弧所在圆的圆心为O,线段AB,CD均与圆弧相切,点B,C分别为切点,已知AB的长10 cm,CD的长为25.2 cm.
(1)如图①,若话筒弯曲后CD与桌面AM平行,此时CD距离桌面14 cm,求弧BC的长度(结果保留π);
(2)如图②,若话筒弯曲后弧BC所对的圆心角度数为60°,求话筒顶端D到桌面AM的距离(结果保留一位小数).(参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
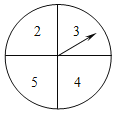
【题目】如图所示,有一个可以自由转动的转盘,其盘面分为4等份,在每一等份分别标有对应的数字2,3,4,5.小明打算自由转动转盘10次,现已经转动了8次,每一次停止后,小明将指针所指数字记录如下:
次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 |
数字 | 3 | 5 | 2 | 3 | 3 | 4 | 3 | 5 |
(1)求前8次的指针所指数字的平均数.
(2)小明继续自由转动转盘2次,判断是否可能发生“这10次的指针所指数字的平均数不小于3.3,且不大于3.5”的结果?若有可能,计算发生此结果的概率,并写出计算过程;若不可能,说明理由.(指针指向盘面等分线时为无效转次.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受地震的影响,某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从两养殖场调运鸡蛋到超市的路程和运费如表:
到超市的路程(千米) | 运费(元/斤千米) | |
甲养殖场 | 200 | 0.012 |
乙养殖场 | 140 | 0.015 |
(1)若某天调运鸡蛋的总运费为2670元,则从甲、乙两养殖场各调运了多少斤鸡蛋?
(2)设从甲养殖场调运鸡蛋x斤,总运费为W元,试写出W与x的函数关系式,怎样安排调运方案才能使每天的总运费最省?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com