
【题目】科技小组进行了机器人行走性实验,在实验场地有![]() 三点在同意笔直的赛道上,
三点在同意笔直的赛道上,![]() 两点之间的距离是540m,甲、乙两机器人分别从
两点之间的距离是540m,甲、乙两机器人分别从![]() 两点出发,甲机器人匀速按
两点出发,甲机器人匀速按![]() 的方向行走,乙机器人按
的方向行走,乙机器人按![]() 方向行走,乙先出发1min,甲再出发,甲、乙离各自出发点的距离
方向行走,乙先出发1min,甲再出发,甲、乙离各自出发点的距离![]() 与乙出发的时间
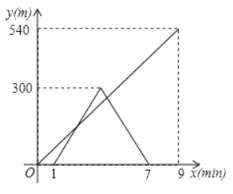
与乙出发的时间![]() 的函数关系式如图所示,结合图像回答下列问题:
的函数关系式如图所示,结合图像回答下列问题:
(1)甲的速度是__________m/min;乙的速度是________m/min;
(2)求甲机器人从C点返回A点时![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)乙机器人出发多长时间后两机器人相距80m.
【答案】(1)100;60;(2)![]() ;(3)乙机器人出发3.5min、6min或
;(3)乙机器人出发3.5min、6min或![]() min时两机器人相距80m.
min时两机器人相距80m.
【解析】
(1)根据函数图象中的数据结合速度=路程÷时间计算即可;
(2)利用待定系数法求解即可;
(3)分三种情况:①当甲车从A到C,两机器人相距80m时,②当甲车从C到A,两机器人相距80m时,③当甲车达到A地后,两机器人相距80m时,分别列方程求解即可.
解:(1)由题意可得,甲的速度为:300÷![]() =100m/min,
=100m/min,
乙的速度为:540÷9=60m/min,
故答案为:100,60;
(2)设y与x的函数关系式为y=kx+b,
∵![]() ,3+1=4,
,3+1=4,
∴函数图象过点(4,300),(7,0),
代入得:![]() ,解得:
,解得:![]() ,
,
∴甲机器人从C点返回A点时y与x的函数关系式为:y=100x+700;
(3)设乙机器人出发tmin时两机器人相距80m,
①当甲车从A到C,两机器人相距80m时,
由题意得:100(t1)+80+60t=540,
解得:t=3.5,
②当甲车从C到A,两机器人相距80m时,
由题意得:54060t80=300[100(t1)300],
解得:t=6,
③当甲车达到A地后,两机器人相距80m时,
由题意得:54080=60t,
解得:t=![]() ,
,
答:乙机器人出发3.5min、6min或![]() min时两机器人相距80m.
min时两机器人相距80m.


科目:初中数学 来源: 题型:
【题目】为全面推进“三供一业”分离移交工作,甲、乙两个工程队承揽了某社区2400米的电路管道铺设工程.已知甲队每天铺设管道的长度是乙队每天铺设管道长度的1.5倍,若两队各自独立完成1200米的铺设任务,则甲队比乙队少用10天.
(1)求甲、乙两工程队每天分别铺设电路管道多少米;
(2)若甲队参与该项工程的施工时间不得超过20天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线相交于O,给出下列 5个条件:①AB∥CD ;②AD∥BC;③AB=CD ;④∠BAD=∠BCD;⑤OA=OC.从以上5个条件中任选 2个条件为一组,能推出四边形ABCD为平行四边形的有( )
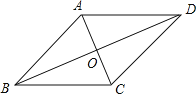
A. 4组 B. 5组 C. 6组 D. 7组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,与反比例函数
,与反比例函数![]() 的图象在第四象限交于点
的图象在第四象限交于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,
,![]() .
.
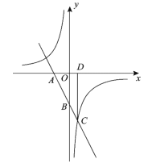
(1)求该反比例函数的表达式;
(2)点![]() 是这个反比例函数图象上的点,过点
是这个反比例函数图象上的点,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,连接
,连接![]() 、
、![]() ,如果
,如果![]() ,直接写出点
,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
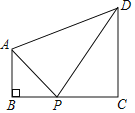
【题目】如图,四边形ABCD中,AB∥CD,∠B=90°,AB=1,CD=2,BC=m,点P是边BC上一动点,若△PAB与△PCD相似,且满足条件的点P恰有2个,则m的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2![]() ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一单位为1的方格纸上,![]() ,
,![]() ,
,![]() …,都是斜边在
…,都是斜边在![]() 轴上,斜边长分别为2,4,6,…的等腰直角三角形,若
轴上,斜边长分别为2,4,6,…的等腰直角三角形,若![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,
,![]() ,
,![]() ,则依图中所示规律,
,则依图中所示规律,![]() 的坐标为( )
的坐标为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
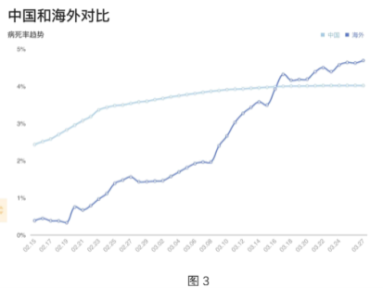
【题目】图1是2020年3月26日全国新冠疫情数据表,图2是3月28日海外各国疫情统计表,图3是中国和海外的病死率趋势对比图,根据这些图表,选出下列说法中错误的一项( )


A.图1显示每天现有确诊数的增加量=累计确诊增加量-治愈人数增加量-死亡人数增加量.
B.图2显示美国累计确诊人数虽然约是德国的两倍,但每百万人口的确诊人数大约只有德国的一半.
C.图2显示意大利当前的治愈率高于西班牙.
D.图3显示大约从3月16日开始海外的病死率开始高于中国的病死率
查看答案和解析>>
科目:初中数学 来源: 题型:
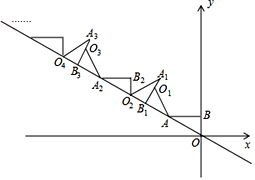
【题目】如图,![]() 轴,垂足为
轴,垂足为![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转到
逆时针旋转到![]() 的位置,使点
的位置,使点![]() 的对应点
的对应点![]() 落在直线
落在直线![]() 上,再将
上,再将![]() 绕点
绕点![]() 逆时针旋转到
逆时针旋转到![]() 的位置,使点
的位置,使点![]() 的对应点
的对应点![]() 落在直线
落在直线![]() 上,依次进行下去......若点
上,依次进行下去......若点![]() 的坐标是
的坐标是![]() ,则点
,则点![]() 的纵坐标为__________.
的纵坐标为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com